1 mole amount of compound A . In a fact: how great amount of free energy belongs to one 1 mol in mixture.
Chemical Potential µ and Homeostasis
2013. Riga Stradin’s University BioChemicalPprocesE.doc
Chemical potential show, how much change of free energy ![]() GA brings into system-reaction adding of
GA brings into system-reaction adding of
1 mole amount of compound A . In a
fact: how great amount of free energy belongs to one 1 mol in
mixture.
It means how much free energy ![]() GA has itself per 1 mole compound A , if
amount of compound in molar numbers
GA has itself per 1 mole compound A , if
amount of compound in molar numbers
is ![]() nA = 1 mole : µA =
nA = 1 mole : µA = ![]() =
= ![]() G°A + R•T•ln(XA) (1-1)
G°A + R•T•ln(XA) (1-1)
chemical potential of compound A, where: ![]() G°A, kJ/mol - standard chemical potential at standard conditions
G°A, kJ/mol - standard chemical potential at standard conditions
T = 298.16 K , pressure p = 101.3 kPa; R = 8.3144 J/mol/K - universal gas constant;
ln(XA) -
natural logarithmic function from argument XA and XA, unless - molar fraction concentration of
compound A, expressed as XA = nA/ntotal and laying
between 0<XA≤1 (absence and pure) compound A
concentrations, where nA, mol - number of moles for
compound A and ntotal , mol - total number of moles
all present compounds total including water. Logarithmic function properties ln(1) = 0 yield that standard
chemical potential ![]() G°A = µA at XA = 1 is pure A compound 1 mol free energy content
G°A = µA at XA = 1 is pure A compound 1 mol free energy content ![]() G°A,
G°A,
assuming standard free energy of formation G°A from elements for compound A per one 1 mole.
Reaction proceeds completely forward until end only when products of reaction have hardly little
disposition
to reverse change back into reactants.
In other words these products of
reaction have trifling remarkable or
zero value of chemical potential: µproducts = 0 , affinity turns back to reactants: A <=x= products .
Thermodynamical conditions of chemical equilibrium.
Provided
chemical potential of reaction products is taking into consideration
(it has anything remarkable level of value ) , then reaction proceeds not
completely until end, go not on completely
100% to reactants conversion to products, but one can observe the setting in
equilibria.
In state of equilibria sum of chemical potentials for
initial compounds is equal to sum of chemical potentials for
products – according chemical reaction equation reactants aA + bB and
products cC + dD:
aA + bB ![]() cC
+ dD ; aµA + bµB = cµC + dµD (1-2)
cC
+ dD ; aµA + bµB = cµC + dµD (1-2)
|
because
compound factor-coefficients a, b, c, and d means multiply µ (B+B+B+...)= bB = bµB; (C+C+C+…)= cC = cµC; (D+D+D+…)=dD=dµD Chemical potencial µ like as amount of The
concentrations X of reactants and products at equilibrium define the equilibrium constant, Keq (see the Chemical Equilibrium).
In the general reaction chemical
potential sum for reactants |
- ![]() G°reaction = R•T•ln
G°reaction = R•T•ln ![]() = R•T•ln(Keq) ; Keq =
= R•T•ln(Keq) ; Keq = ![]() (1-3)
(1-3)
Kaksis 2011. Riga Stradin’s University http://aris.gusc.lv/BioThermodynamics/ChemicalPotential.doc
![]() Greaction =
Greaction = ![]() G°reaction + R•T•ln
G°reaction + R•T•ln  ≠0
; 0 =
≠0
; 0 = ![]() G°reaction + R•T•ln(Keq)
at equilibrium zero (1-4)
G°reaction + R•T•ln(Keq)
at equilibrium zero (1-4)
in Homeostasis(XDd•XCc)/(XAa•XBb)≠Keqdiffers from equilibrium constant Keq = ![]()
We must be careful to distinguish
between two 2 different quantities:
the free-energy change, ![]() G, and the
G, and the
standard free-energy change, ![]() G°. Each chemical reaction has a
characteristic standard free-energy
change per
G°. Each chemical reaction has a
characteristic standard free-energy
change per
one 1 mol of reactant, which maybe positive ![]() G°>0, negative
G°>0, negative ![]() G°<0, or some times zero
G°<0, or some times zero ![]() G°=0, depending on
G°=0, depending on
the equilibrium constant Keq of the reaction. The standard free-energy change ![]() G° tells us in which direction
G° tells us in which direction
and how far a given reaction must go to reach equilibrium when the temperature is 25 °C or
To = 298.15 K, and the
pressure p is 101.3 kPa (1 atm) and
component concentrations at equilibrium are X.
Thus ![]() G° is a constant: it has a
characteristic, unchanging value for a given reaction. But the actual free-energy
G° is a constant: it has a
characteristic, unchanging value for a given reaction. But the actual free-energy
change ![]() G, is a function of reactant and product concentrations X and of the temperature T = 310.15 °K
G, is a function of reactant and product concentrations X and of the temperature T = 310.15 °K
prevailing during the reaction in human body, which will not necessarily match
the standard conditions as
defined above. Moreover, the ![]() G of any reaction proceeding => spontaneously toward
its equilibrium state is
G of any reaction proceeding => spontaneously toward
its equilibrium state is
always negative ![]() G<0, becomes less negative as the
reverse <= reaction
proceeds, and is zero
G<0, becomes less negative as the
reverse <= reaction
proceeds, and is zero ![]() G=0 at the point
G=0 at the point
of equilibrium (XDd•XCc)/(XAa•XBb) = Keq, indicating that no
more work W = -![]() G = 0 can
be done by the
G = 0 can
be done by the
reaction: aA + bB = cC + dD according expression ![]() G°reaction + R•T•ln(Keq)=0 (1-4).
G°reaction + R•T•ln(Keq)=0 (1-4).
Studies in „Medical
chemistry”, „Biochemistry”. Studies of Gibs free energy changeΔGreac = ΔHreac – T ·ΔSreac
ΔHreac |
ΔSreac |
T |
ΔGreac |
Spontaneous ability of reaction |
Dispersed energy T·ΔSreac>0 is bound in surrounding and is lost as used free energy ΔGreac<0 |
|
|
|
Biochemical catabolism in living organisms consume the free energy in spontaneous reactions maintain organisms living. |
Endothermic Positive ΔHreac>0 |
low T ΔHreac>|-T·ΔSreac| |
Positive ΔGreac>0 ΔHreac–T·ΔSreac>0 |
unfavorable reaction at low temperature |
|
ΔHreac<|-T·ΔSreac| |
ΔHreac–T·ΔSreac< 0 |
|
||
2. Negative ΔHreac<0 |
consume free energy change ΔGreac<0 for life mantanance of organisms 37º C in human as well as to supply the heat for organisms as reaction Exothermic ΔHreac<0 |
high T |
|
|
Living cell proliferations and existing conditions for Life |
ΔSreac<0 Negative entropy decreases entropy change is negative |
synthesis reaction |
A + B =>AB |
ΔSreac<0 Negative |
3. Positive ΔHreac>0 |
|
|
|
|
Negative ΔHreac<0 |
in synthesized molecules, living cells live and proliferates |
|
Positive ΔGreac>0 ΔHreac–T·ΔSreac>0 |
|
low T |
Negative ΔGreac<0 ΔHreac–T·ΔSreac<0 |
spontaneous reaction at low temperature |
In life important are negative change ΔSreac<0 of entropy and positive increase ΔGreac>0 of free energy!
A.Kaksis 2005. Riga Stradin’s University 4th page http://aris.gusc.lv/BioThermodynamics/BioThermodynamics.doc
Three Reaction examples studies of Homeostasis for students Medical (Bio)Chemistry :
red and blue light photons energy E=hν absorbtion heat accumulates in glucose substance ΔHreac>0 EndothermicΔHreac=+2805,27 kJ/mol 6 H3O++ 6 HCO3-+Q+ΔGreac=+2970 kJ/mol Endoergic ΔGreac=+2970 kJ/mol photosynthetic proces ΔGreac>0 is free energy accumulates in 1 mol cytosolic glucose molecules C6H12O6 biochemically „combusted” by oxygen O2 in mitochondria to combustion products CO2 and H2O along oxidative phosphorilation pathway. |
———————=>  reverse reaction |
<=---Photo synthetic <=-Reaction <=--- Center oxygen C6H12O6+ 6 O2 + 6 H2O Glucose biochemical „combustion” Glycolysis, Oxidative Phosphorylation |
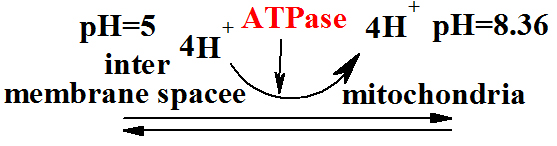
The Membrane potential 3rd page http://aris.gusc.lv/BioThermodynamics/MembraneElektrodsAM.doc
(page 9 http://aris.gusc.lv/BioThermodynamics/OxRedBiologicalW.doc)
ADP3- +H2PO4- |
|
For free
energy ΔGreac=+17.2 kJ/mol accumulation
![]()
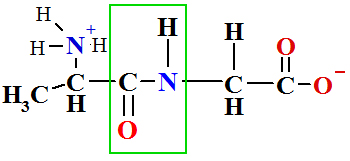
in Peptide Bond Formation Reaction is The Ribosomal protein synthesis: ala + gly®ala-gly+ H2O.
To store free energy ΔGreac=+17.2 kJ/mol per one mole of peptide bond.
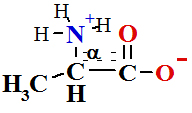
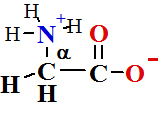
|

ΔG = -30.5kJ/mol and total reaction sum is ΔGreac =+17.2 + (- 30.5)= -13.3 kJ/mol |
|