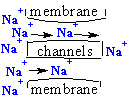Aris Kaksis 2011. Riga University
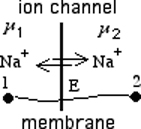
The Membrane equilibrium potential obtaining for the ions H+, Na+, K+, HCO3- and Cl-.
G
= G2 - G1
|
|
|
One 1 mol of the sodium
ions with charge n=+1 from inside Cell transfer from left side => to right side
thru membrane channels form outside Cell of the sodium ions
concentration is the standard free energy
change performed work Wwork of one mol Na+ transfer from point 1 inside Cell to point 2 outside Cell
solution applied with negative value -° at electric potential value E.
One mole Na+ charge is ion charge n=+1 by faradays number F=96485 C
respectively q = nF , and work calculated as W work = qE = nFE = - G° = RTlnKeq
membrane equilibrium
constant Keq=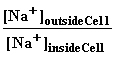
so
Emembrane=
•ln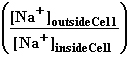
and E=0 if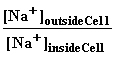=1
Nernst's
equation in natural (number e=2) logarithm ln and decimal (number
10) logarithm lg form
ln(a) = ln(10)·lg(a)= 2,3...·lg(a). Temperature at standard
conditions are T=298.15 K and R=8.3144 J/mol/K.
E =•ln;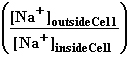
ln(10)•R•T/F=2.3•R•T/F=0,0591 V ;
E=0.0591/n•lg,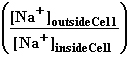
where n is the charge of ion (for sodium cation Na+ n=+1,
for potassium cation K+ n=+1, for chloride anion Cl- n=-1,
for bicarbonate anion HC3- n=-1 and for hydrogen ion H+ n=+1 and so on, so on).
Second (correct) approach to obtaining membrane potential expression.
We are observing from
inside Cell motion of one mole n charged ions with total molar charge q = nF
thru the membrane channels and wen equilibrium is established reactant and
product chemical potential
sum becomes equal across Cell membrane 
Na+insideCell + nFE = Na+outsideCell
but each
chemical compound chemical potential is: = G° + RTln(NA) , were NA is
substance A
concentration in molfraction units. G° is given compound A standard potential of
formation from elements.
In chemical equilibrium given compounds sodium cation have G°Na+and G°Na+ are equal.
G°Na+ +
RTln(NNa+insideCell) + nFE = G°Na+ +
RTln(NNa+outsideCel)
Expressing E from equilibrium conditions of the chemical potentials µ :
Emembrane =
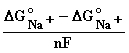+ •ln .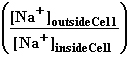
Standard potentials of pure sodium ions one mol are equal and membrane potential is
Emembrane = •ln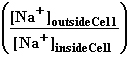. as 0 = .
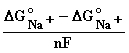conversion to molar
concentrations and decimal logarithm we
obtain
Na+ insideCell
.
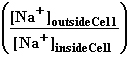For Physiological
conditions T= 310.15 K and Emembrane = 0.06514/n
.
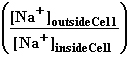Table. Concentration of some ions inside and outside mammalian spinal motor neurons. pHinsid=6.826
|
Concentration |
Equilibrium Potential (mV) |
|
|
Inside Cell |
Outside Cell |
|||
Na+ |
15.0 |
150.0 |
+61.54 |
|
K+ |
150.0 |
5.5 |
-88.35 |
|
10-7·c H+ |
14.93 |
4.365 |
-32.87 |
|
Cl- |
9.0 |
125.0 |
-70.32 |
|
HCO3- |
27.0 |
8 |
+32.51 |
A- organic anions (phosphorilated organic—OPO3- |
A- |
122.49 |
43.79 |
+27.49 |
Total Resting membrane potential E = -70 mV. and carboxylic organic—COO-) .
Membrane potential for sodium cations Na+ is calculated according membrane potential expression
Membrane potential E = 0.06514/+1•lg
Membrane potential for potassium K+ cations is calculated according membrane potential expression
Membrane potential E = 0.06514/+1•lg(5.5/150) = -88.35 mV ;
Membrane potential for hydrogen H+ cations is calculated according membrane potential expression
Membrane potential E = 0.06514/+1•lg(4.365/14.93) = -32.87 mV at outside Cell pH=7.36 c=4.365·10-7 M;
Membrane potential for chloride Cl- anions is calculated according membrane potential expression
Membrane potential E = 0.06514/-1•lg(125/9) = -70.32 mV ;
Membrane potential for bicarbonate HC3- anions is calculated according membrane potential expression
Membrane potential E = 0.06514/-1•lg(8/27) = +32.51 mV ;
Membrane potential for organic anions A- anions is calculated according membrane potential expression
Membrane potential E = 0.06514/-1•lg(43.79/122.49) = +27.49 mV .
Table. Steady-state membrane potential of mammalian skeletal muscle.1
Ion |
Concentration c (mmol/L of H2O) |
Equilibrium Potential (mV) |
|
Inside Cell |
Outside Cell |
||
Na+ |
12.0 |
145.00 |
+66.60 |
K+ |
155.0 |
4.00 |
-97.74 |
10-5·c H+ |
13.0 |
3.80 |
-32.87 |
Cl- |
3.8 |
120.00 |
-92.27 |
HCO3- |
27.0 |
8.00 |
+32.51 |
A- |
155.0 |
43.79 |
+33.7 |
Total Resting membrane potential E = -90 mV .
Mitochondria have active value of pH = 8.36 inside and pH = 5 in extra mitochondrial space.
Bicarbonate concentration in cytosole-blood [HCO3-]+[CO2]=0.023M and [HCO3-]=0.015M and
using Hendersone Hasselbah equation calculated concentration CO2 [CO2] we can express:
pH=pK+lg([HCO3-]/[CO2]); 7.36=7.0512+lg([HCO3-]/[CO2]) and antilogaritming
is calculated concentration of carbon dioxide in blood, cytosole and mitochondria.
Inside pH = pK+lg([HCO3-Mitochon]/[CO2]);
8.36 = 7.0512+ lg([HCO3-Mitochon]/[CO2])
respectively 108.36-7.0512=[HCO3-Mitochon]/[CO2] = 20.36 = [HCO3-Mitochon]/0.0076M
and inside Mitochondria bicarbonate concentration is
ten times higher [HCO3-]= 20,36·0.0076M = 0.154 M .
Human body temperature t=37°C ; T = 310.15° K.
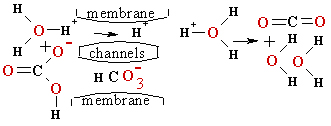
Actual membrane potential for hydrogen cations H3O+ via
the membrane penetrating proton and
bicarbonate HCO3- channels reveal the equilibrium H3O+Mitochon 
span> H3O+extraMit and
EH+membr=P·lg(10-pH extraMit/10-pHMitochon)=0.06154·lg(10-5/10-8.36)=P·lg(103.36)=0.2068V.
Actual membrane potential for bicarbonate
anions equilibrium HCO3-Mitochon HCO3-cytosole is
EHCO3-Mitochon,=-P·lg([HCO3-cytosole]/[HCO3-Mitochon])= -0.06154·lg(0.0154/0.154)= 0.06154 V ,
where P =ln(10)•R•T/F = ln(10)•8.3144(J/mol/K)•310.15 K / 96485 C =0.06154 V, at constant T=310,5°C
Hydrogen and bicarbonate total membrane potential is Emembr=0.2722V=0.2068V+0.06154V.
Electric free
energy change G
per one mole of proton H+ drive ATPase to make work is
G
= - ExF=-0.2722·96485=-26263J/mol=
-26.3 kJ/mol and is very effective
per one mol mass one gram
of proton H+ in direction from extra membrane space (H3O+extraMit) to mitochondrial matrix space (H3O+Mitohon).
(page 9 http://aris.gusc.lv/BioThermodynamics/OxRedBiologicalW.doc).
The concentration gradient chemical free energy change (P·96485= 5937.7
J/mol)
G<
=P·96485·lg([H+]Mitohon/[H+]extraMit)=
-19.95 kJ/mol with proton H+ gradient drive ATPase nano engine
to synthesizing ATP molecules.
Both free energy
changes sum per one mole of protons is -46.214
kJ/mol , which drive ATPase nanoengine
rotation to synthesizing one ATP molecule, consuming four protons 4 H+ .
One mole ATP
G<
= - 4x46.214
kJ/mol= -184.85 kJ/mol.
Macroergic ATP phosphate anhydride bond in hydrolyze releases free
energy G
= -53.47
kJ/mol for human erythrocyte
(page13 http://aris.gusc.lv/BioThermodynamics/BioThermodynamics.doc).
In ATP accumulated chemical free energy efficiency is 28.9% (-53.47
kJ/mol) of theoretically consumed efficiency
100% (-184.85 kJ/mol) using
oxidative phosphorilation. 71.1% of used four proton chemiosmose energy
consumes
the friction of ATPase rotor and ATP transportation movement in water medium.
Were any other
charged cation molecule, for example, Na+ cation 23 times heavier or
potassium cation K+ 39
times heavier and its relatively les efficiency per one gram of mass are
transferred 23 times or 39 times les energy
for ATP synthesis of charged cation as for proton H+.
Nature choose the best small by size, by mass and bearing whole one unit positive charge proton ion H+.