Chemistry Biochemistry and Bio-Medical Sciences
Aris Kaksis 2016.
Riga Stradin's
University
The Oxidation Reduction of Biological Systems
BioThermodynamics.doc
OxRedBiologicalW.doc
Biological Oxidation-Reduction Reactions
The transfer of phosphoryl
groups is a central feature of metabolism. Equally important is
another kind of transfer,
electron transfer in oxidation-reduction(OxRed) reactions. These reactions
involve the loss of electrons -e- by one
chemical species, which is thereby oxidized, and the gain of electrons +e - by another, which is reduced. The flow of
electrons => e- in oxidation-reduction (OxRed) reactions is responsible, directly or indirectly, for all work (W) done
by living organisms. In non-photo synthetic organisms, the sources of
electrons e- are reduced compounds (foods);
in photo synthetic organisms, the initial electron -e-donor is a chemical species excited by the absorption A
of light ~hv = E energy. The path of electron - e-
flow => in metabolism is complex.
Electrons e- move from => various metabolic intermediates to => specialized
electron e- carriers in enzyme -
catalyzed reactions. The carriers e- in turn donate electrons e- to acceptors with higher
electron e- affinities, with the release of energy.
Cells contain a variety of molecular energytransducers, which
convert the energy of electron e- flow
into useful work: W = E•F•n ; where,
E potential between species (in volts V); F = 96485 C (coulomb) 1 mol of electrons e- electric
charge in C;
n number of electrons e- involved in
species OxRed reactions - between oxidised state (Ox) and
reduced state (Red) of compound. Established so called OxRed system with own RedOx potential E :
Ox + n
e-  Red ; E = E°+
Red ; E = E°+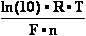 •lg
•lg (1)
(1)
where E° - standard potential of given OxRed system measured at
conditions when E = E° (as [Ox] = [Red]);
natural logarithm of number 10 - ln(10) = 2.302585093 ;
universal gas constant - R = 8.3144 J/mol/K ;
absolute thermodynamics temperature T = 273.16° + 25° C = 298.16
K at standard temperature conditions measured:
as Kelvin scale value 273.16 K at zero 0°C point plus on Celsius
scale measured 25°C but human body temperature
37°C that will be higher T = 273.16° + 37°(C) = 310.16
K non-standard conditions;
Faraday's constant - F = 96 485 C (coulomb) 1 mol of
electrons e- electric charge in C;
number of electrons e- involved in OxRed system - n ; decimal logarithmic function - lg( ) of argument as
ratio
([Ox]/[Red]) between oxidised form concentration - [Ox] as
multiple over reduced form concentration [Red].
We begin our discussion with a description of the general types of metabolic reactions in which electrons e- are
transferred. After considering the theoretical and experimental basis for
measuring the energy changes  G in
G in
oxidation reactions in terms of electromotive force (EMF),
we discuss the relationship between this force,
expressed in volts V, and the free-energy change  G , expressed in joules J. We conclude by
describing the
G , expressed in joules J. We conclude by
describing the
structures and oxidation-reduction chemistry of the most common
of the specialized electron e- carriers =>,
which you will encounter repeatedly in later discussions.
The Flow of
Electrons can do Biological Work
Every time we use a motor,
an electric light or heater, or a spark to ignite gasoline in a car engine, we use
the flow => of electrons e- to accomplish
work W=E•F•n, where n (in units mol) is
the electron number
of moles moving from reduced form Red => to oxidised form Ox . In the circuit that powers a motor, the source
of electrons e- can be a battery containing two 2 chemical species that differ in affinity for
electrons e- .
Electrical wires provide a pathway for electron e- flow => from the chemical species reduced form Red1
at one pole (-) of the battery, through the motor, to the
chemical species oxidized form Ox2 at the other
second 2nd pole (+) of the battery.
(-) Red1  Ox1 + n
e- => Electrical wires number n electrons n
e- - flow => Ox2 + n
e-
Ox1 + n
e- => Electrical wires number n electrons n
e- - flow => Ox2 + n
e-  Red2 (+)
Red2 (+)
- E1 electron-carriers in biological systems n electrons n
e- flow => E2
for closed circuit electric-motion force is calculated as sum EMF = E1 - E2 in volts V .
Because the two 2 chemical species differ in their affinity for
electrons e- , electrons e- flow => spontaneously
through the circuit, driven by a force proportional to the
difference in electron e-affinity, the
electro-motive force (EMF ). The electromotive force (typically a few volts ±1÷3.5 V) can accomplish work
W=EMF•F•n if an appropriate energy transducer in this case a motor is placed in the circuit. The motor can be
coupled to a variety of mechanical devices to accomplish useful work W = EMF•F•n.
Living cells have an analogous
biological ''circuit,'' with a relatively reduced compound such as glucose as
the source of electrons e- . As glucose is enzymatic oxidized, the electrons e- released flow => spontaneously
through a series of electron-carrier intermediates to another chemical
species, such as O2.
This electron e- flow => is ex-ergonic because O2 has a higher affinity for electrons e- than do the
electron- -carrier intermediates. The resulting electro-motive force provides energy to a variety of molecular energy
transducers (enzymes and other proteins) that do biological
work W. In the mitochondrion, for example,
membrane-bound enzymes couple electron e- flow => to the production of a trans-membrane
pH difference
 pH=8.36-5.00=3.36,
accomplishing osmotic and electrical work. The proton H+ gradient thus formed has
pH=8.36-5.00=3.36,
accomplishing osmotic and electrical work. The proton H+ gradient thus formed has
potential energy, sometimes called the proton-motive force by
analogy with electro-motive force. Another enzyme,
ATP synthase in the inner mitochondrial membrane, uses the proton-motive
force Emembrane to do chemical work W:
synthesis of ATP from ADP and Pi as protons H+ flow => spontaneously across the membrane.
Similarly, membrane-localized enzymes in E. coli convert electro-motive
force to proton-motive force, which is then
used to power flagella motion.
The principles of electrochemistry that govern energy changes in the macroscopic circuit with a motor and battery
apply with equal validity to the molecular processes accompanying electron e- flow => in living cells. We turn now
to a discussion of those principles.
Oxidation-Reductions Can Be
Described as Half-Reactions of two Ox  Red Systems
Red Systems
Although oxidation and reduction must occur together, it is convenient when describing electron e- transfers =>
to consider the two 2 halves (OxRed systems) of an oxidation-reduction reaction separately. For example,
the oxidation of ferrous ion Fe2+ by cupric ion Cu2+,
Fe2+ + Cu2+ => Fe3+ + Cu+ can be described in terms of two 2 half-reactions (Ox  Red systems):
Red systems):
(1) Fe2+  Fe3+ +
e- The electron-donating e- molecule in an oxidation-reduction reaction is called
Fe3+ +
e- The electron-donating e- molecule in an oxidation-reduction reaction is called
(2) Cu2+ +
e-  Cu+ the reducing agent or reductant;
the electron-accepting + e- molecule is the oxidizing
Cu+ the reducing agent or reductant;
the electron-accepting + e- molecule is the oxidizing
agent or oxidant. A given agent, such as an iron cation existing
in the ferrous (Fe2+) or ferric (Fe3+)
state, functions
as a conjugate reductant-oxidant pair (RedOx pair), just as an acid and corresponding base function
as a conjugate acid-base pair. Recall from
Acid-Base Equilibrium that in acid-base reactions we can write a
general equation:
proton donor  H+ + proton acceptor.
H+ + proton acceptor.
In RedOx reactions we can write a similar general equation:
electron donor  n
e- + electron acceptor.
n
e- + electron acceptor.
In the reversible half reaction (1) above, Fe2+ is the
electron donor and (2) Fe3+ is the electron acceptor;
together, Fe2+ and Fe3+ constitute a conjugate
RedOx pair.
The electron e- transfers in the oxidation-reduction reactions of organic compounds are
not fundamentally different
from those of inorganic species. In Reducing Sugars we considered the oxidation of a reducing sugar
(an free aldehyde or ketone) by cupric ion Cu2+(see reducing
sugars):
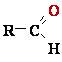 +
4 OH- + 2 Cu2+
+
4 OH- + 2 Cu2+
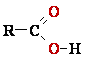 + Cu2O + 2 H2O
+ Cu2O + 2 H2O
This overall reaction can be expressed as two 2 half-reactions using OxRed systems:
(1)
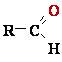 + 2
OH-
+ 2
OH-
 + 2 e- +
H2OBecause two 2 electrons 2 e- are removed from the
+ 2 e- +
H2OBecause two 2 electrons 2 e- are removed from the
(2) 2 Cu2+ + 2 e- + 2
OH- Cu2O + H2Oaldehyde
carbon —(C=O)—H, the second 2nd half-reaction
Cu2O + H2Oaldehyde
carbon —(C=O)—H, the second 2nd half-reaction
(the one-electron reduction of cupric Cu2+ to cuprous ion Cu+) must be doubled 2 to balance the overall equation
two 2 electrons 2 e- are gained on two cupric Cu2+ cations converting
to two cuprous ions Cu+.
Biological
Oxidations Often Involve Dehydrogenation
The carbon in living cells
exists in a range of oxidation states (Fig. 1). When a carbon atom
shares an electron pair :
with another atom (typically H, C, S, N, or O),
the sharing is unequal in favor of the more electronegative atom.
The order of increasing electronegativity: H < C < S < N < O respectively 2.2 < 2.55 < 2.58 < 3.04 < 3.44.
In over simplified but useful terms, the more electronegative atom ''owns''
the bonding electrons e- it shares with
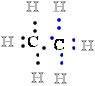
another atom. For example, in methane (CH4)
carbon C is more electronegative than the four 4 hydrogens H bonded
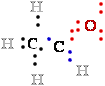
to it, and the C atom therefore ''owns'' all eight 8 bonding electrons 8 e- (Fig. 1). In ethane, the
electrons e-
in the  C-C
C-C bond are shared equally, so each :::C:C::: atom owns only seven 7 of its eight 8 bonding electrons e-.
bond are shared equally, so each :::C:C::: atom owns only seven 7 of its eight 8 bonding electrons e-.
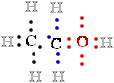
In ethanol, C-1 is less electronegative than the oxygen O to which it is bonded, and the O atom therefore ''owns''
both electrons 2 e- of the  C-:O- bond, leaving ::.C-1 with only
five 5 bonding electrons e-. With each formal loss
C-:O- bond, leaving ::.C-1 with only
five 5 bonding electrons e-. With each formal loss
of electrons e-, the carbon C atom has undergone oxidation even when no oxygen O is involved, as
in the conversion
of an alken (CH2=CH2) to an alkyne (CH CH).
In this case, oxidation (loss of electrons e-) is
coincident with
CH).
In this case, oxidation (loss of electrons e-) is
coincident with
the loss of hydrogen - H. In biological systems, oxidation is
often synonymous, with dehydrogenation, and many
enzymes that catalyze oxidation reactions are dehydrogenases. Notice that the more reduced compounds in Figure 1
(top) are richer in hydrogen H than in oxygen O, whereas the more oxidized compounds (bottom) have
more oxygen O
and less hydrogen H.
Not all biological oxidation-reduction reactions involve carbon C. For example, in the conversion of molecular
nitrogen N2 to ammonia NH3 : 6 H+ + 6 e- + °N2=> 2 (-3)NH3,
the nitrogenN atoms are reduced.
Electrons e- are transferred => from one molecule (electron e-donor) to another (electron e-acceptor) in
one 1 of four 4 different ways:
1. Directly as electrons e-.
For example, the Fe2+/Fe3+RedOx pair can transfer an
electron e- to the
Cu+/Cu2+RedOx pair: Fe2+ + Cu2+=> Fe3+ + Cu+
2. As hydrogen H atoms. Recall that a hydrogen H atom consists of a proton H+ and a single electron e-.
In this case we can write the general equation: AH2=> A + 2 e- + 2 H+
where AH2 is the hydrogen/electrondonor.
(Do not mistake the above reaction for an acid dissociation;
the H+arises from the
removal of a hydrogen atom
(H+ + e-).) AH2 and A together constitute a conjugate RedOx pair (A / AH2), which can reduce another
compound
B (or RedOx pair, B / BH2) by transfer of hydrogen H atoms: AH2 + B => A + BH2
3. As a hydride ion (:H-),
which has two 2 electrons e-.
This occurs
m the case of NAD-linked dehydrogenases, described below.
4. Through direct combination with oxygen O2.
In this case, oxygen O2 combines with an organicreductant and is
covalently incorporated in the product, as in the oxidation of a
hydrocarbon to an alcohol by
1/2 O2 presented as O: R-CH2-H + .:O:. => R-CH2-::O::-H
The hydrocarbon is the electron e-donor and the oxygen O atom is the electron e-acceptor.
All four 4 types of
electron e- transfer occur in cells. The neutral term reducing
equivalent is commonly used
to designate a single 1 electron e- equivalent participating in an oxidation-reduction reaction, no matter whether
this equivalent is an electron e- per se, a hydrogen H (H+ + e-)
atom, or a hydride ion :H-,
or whether the electron e-
transfer takes place in a reaction with oxygen O to yield an oxygenated product. Because biological fuel molecules
are
usually enzymatic dehydrogenated to lose two 2reducing
equivalents at a time, and because each oxygen O
atom can accept two 2reducing equivalents, biochemists by
convention regard the unit of biological oxidations as
two 2 reducing equivalents passing from substrate => to oxygen O.
Methane |
 |
8
|
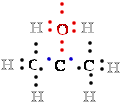
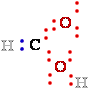
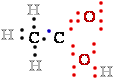
Figure 1. Oxidation states of carbon C occurring in the biosphere.
The oxidation states are illustrated with some representative compounds.
Focus on the black carbon C atom and its bonding
electrons e-. When this carbon C is bonded to the
less |¬ electronegativeH atom, both bonding electrons
(blue - : •) are assigned to
the carbon C.
When carbon C is bonded to another carbon C,
bonding electrons e- are shared equally, so one blue • of the two 2 electrons e-e- is assigned to the black carbon C. When the black carbon C of
our interest is bonded to the more electronegativeO atom, the bonding electrons e- are assigned to the oxygen O:.
The number to the right of each compound is the number n of electrons e- ''owned'' by the black carbon C of our interest, a rough expression of the oxidation state of that carbon C.
When the black carbon C undergoes oxidation (loses
electrons e-), the
number n |<= gets smaller.
Thus the order of increasing oxidation state is alkane <
methane <
< alkane <
< alkene <
< alcohol <
< alkyne <
< aldehyde <
< ketone <
< formic acid <
< carbon mondioxide.
< carboxylic acid
<
< carbon dioxide. |
Ethane (alkane) |
 |
7
|
Ethene (alkene) |
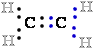 |
6
|
Ethanol 7
(alcohol)
|
 |
5
|
Acetylene (alkYne) |
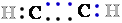 |
5
|
Formaldehyde
|
 |
4
|
Acetaldehyde
(aldehyde) 7 |
 |
3
|
Acetone (ketone) 7 2
|
 |
2
|
Formic acid (carboxylic acid)
|
 |
2
|
Carbon monoxide
|
 |
2
|
Acetic acid (carboxylic
7 1
acid)
|
 |
1
|
Carbon dioxide
|
 |
0
|
Reduction Potentials Measure Affinity for
Electrons
When two 2 conjugate RedOx pairs are
together in solution, electron e- transfer from the electron e-donor of one RedOx pair to the electron e-acceptor of
the other may occur spontaneously. The tendency for such a reaction depends on
the relative affinity of the electron
e- acceptor of each RedOx pair for electrons e-.
The standard reduction
potential, E° a measure (in volts V) of this affinity, can be determined in an experiment such
as that described in Figure 2. Electrochemists have chosen as a standard of reference the half-reaction
H+ + e- H |¬(Pt) , (1/2 H2)
Hydrogen saturated platinum (Pt) H2is a solid metal - first I type electrode n=1 .
H |¬(Pt) , (1/2 H2)
Hydrogen saturated platinum (Pt) H2is a solid metal - first I type electrode n=1 .
E=E°+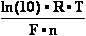 •lg([H3O+]); because of Brønsted water
protonation H+ + H2O=> H3O+
(2)
•lg([H3O+]); because of Brønsted water
protonation H+ + H2O=> H3O+
(2)
E = -0.05916•pH ; because -lg([H3O+]) = pH , and 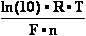 = 0.05916 V at standard conditions (3)
= 0.05916 V at standard conditions (3)
The electrode at which this half-reaction occurs (called a half-cell) is arbitrarily assigned a standard
reduction potential
E° of 0.00 V. When this hydrogen electrode is connected
through an external circuit to another half-cell in which an
oxidized species and its corresponding reduced species are
present as pure H2 compound at standard concentrations C
(each solute at 1 M, each
gas at 101.3 kPa or 1 atm), electrons e- tend
to flow through the external circuit from
the half-cell of lower |¬ standard reduction potential E°1 to the half-cell of higher standard reduction potential E°2.
By convention, the half-cell with the stronger tendency to acquire electrons e- is
assigned a positive value of E°2 > 0.00 V.
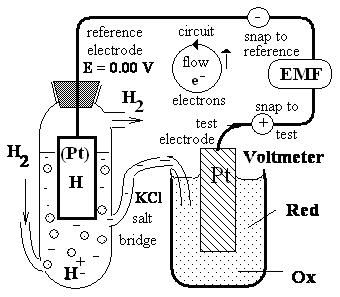
hydrogen electrode
Test cell containing
pure H2 gas at standard pH=7 concentration
pressure saturates
of
the oxidized [H+]
platinum Pt metal with and reduced H(Pt)
H hydrogen forming
(like solide as left)
reference cell with
species of the RedOx
known E = 0.00V
pair to be examined
|
Voltmeter the device for measuring emf conected to refrence snap
and test snap Figure 2. Measurement of the standard
reduction potential (Eo) of a RedOx pair at pH=7 condition. Electrons e- flow => from the test electrode to the reference electrode if standard reduction
potential is negative Eo < 0.00 V or vice versa if positive Eo > 0.00 V. The ultimate reference half-cell is the hydrogen electrode, as shown
here. Electro-chemists have chosen as a standard of reference the half-reaction which this half-reaction occurs is
arbitrarily assigned a standard reduction potential E=E° of 0.00
V pH=0. The electro-motive force (EMF=Eo-E) at pH=7, E of or the hydrogen electrode RedOx system H++ e- H |¬(Pt) is -0.41412V=Eo=-0.05916•pH and EMF=-0.41412-0.0V . H |¬(Pt) is -0.41412V=Eo=-0.05916•pH and EMF=-0.41412-0.0V .
The direction of electron e- flow => depends
on the relative electron ''pressure'' or potential of the two 2 cells.
A salt bridge containing a saturated KCI solution provides a
path for counter-ion movement between the test cell and the reference cell. From the observed emf and the known E = 0.00 V for reference cell, the Eoof the test cell containing the RedOx pair is obtained as calculation EMF + E = Eo = -0.41412 V. The cell that gains
electrons has, by convention, the more positive E > Eoreduction potential and so as well as E = 0.00
V > -0.41412 V = Eo. |
The reduction potential E of a half-cell depends not only on the chemical species present but also
on their activities,
approximated by their concentrations C. About a century ago, Walther
Nernst derived an equation that relates standard
reduction potential (E') to the reduction potential (E)
at any concentration of oxidized [Ox] and reduced [Red] species
in the cell:
Table 1. Standard Reduction Potentials Eo and EM of Some Biologically
Important Half-Reactions, at 37 °C for
pH=7.36 and 8.37 (in mitochondria), E° at standard conditions 298.16 K, pH=0
for H+/ H reference
electrode E°=0.00 V, E°H2O corrected to water concentration [H2O] =
997.07/18.0153 = 55.3457 M
from equations where involved, and E°37. at body temperature conditions 310.16 °K (37
°C) calculated from E°H2O
Half-reaction - OxRed systems
Data source |
Eo(V) |
EM(V) |
E°(V) |
E°H2O(V) |
E°37(V) |
H2O2+2 H3O++
2 e- = 4 H2O
Suchotina |
1.7356 |
1.6734 |
1.776 |
1.9821 |
1.9742 |
O2-+2 H3O++
e- = H2O2+ 2 H2O David Harris |
0.305 |
0.1806 |
1.2764 |
1.48246 |
1.4251 |
O2g+4 H3O+++
4 e-= 6 H2O Suchotina |
0.813 |
0.751 |
1.2288 |
1.38334 |
1.3732 |
NO3-+3H3O++2e-=HNO2+4H2O
University
Alberta |
0.2889 |
0.1957 |
0.9275 |
1.13355 |
1.1291 |
NO3-+ 2 H3O++2e-= NO2-+ 3 H2O David Harris |
0.3913 |
0.3291 |
0.8351 |
0.98967 |
0.95138 |
p-quinone+2H3O+ +2e-=Hydroquinone+2H2O |
0.2336 |
0.1714 |
0.6994 |
0.80243 |
0.79365 |
O2aq+2H3O++2e-=H2O2aqua+
2H2O University
Alberta |
0.2336 |
0.1715 |
0.6945 |
0.7975 |
0.7937 |
Fe3+ + e- = Fe2+
University
Alberta |
0.783 |
0.783 |
0.7690 |
0.7690 |
0.7830 |
Ubiquinone+2H3O+ +2e-=Ubiquinol+2H2O |
0.0197 |
0.0819 |
0.4591 |
0.56215 |
0.5404 |
Fumarate2-+2H3O+ +2e-=Succinate2-+2H2O |
0.0332 |
0.0953 |
0.4451 |
0.54815 |
0.52695 |
CrotonylCoA+2H3O++2e-=ButyrylCoA+2H2O |
-0.0774 |
-0.1395 |
0.3991 |
0.50215 |
0.48273 |
C6H6O6+2H3O+ +2e-=AscorbicAcid+2H2ODC.Harris |
-.0862 |
-.1483 |
0.3900 |
0.4930 |
0.47395 |
Glyoxylate+2H3O++2e-=glycolate+2H2OD.C.Harris 25°C |
-0.111 |
-0.171 |
0.324 |
0.42715 |
0.42715 |
Cytochrome F Fe3+ + e-= Fe2+
David Harris |
0.3509 |
0.3509 |
0.3650 |
0.3650 |
0.3509 |
[FeIII(CN)6]3-+ e-= [FeII(CN)6]4- University
Alberta |
0.3258 |
0.3258 |
0.3557 |
0.3557 |
0.3258 |
Oxalo-acetate2-+2H3O+ +2e-=Malate2-+2H2O |
-0.2225 |
-0.2847 |
0.2481 |
0.35115 |
0.33757 |
Cytochrome a3 Fe3++ e-= Fe2+ |
0.3365 |
0.3365 |
0.3500 |
0.3500 |
0.3365 |
Pyruvate-+2H3O+ +2e-=lactate-+2H2O |
-0.2408 |
-0.3030 |
0.2291 |
0.33215 |
0.3193 |
FADfree+2H3O+ +2e-=FADH2 +2H2O
* |
-0.2735 |
-0.3356 |
0.1951 |
0.29815 |
0.28662 |
CH3CHO+2H3O++2e-=CH3CH2OH+2H2OKortly
Sh |
-0.2784 |
-0.3406 |
0.1900 |
0.2930 |
0.28169 |
Cytochrome a Fe3+ +e-= Fe2+ |
0.2788 |
0.2788 |
0.290 |
0.290 |
0.2788 |
GlutaS-Sthione+2H3O+ +2e-=2GlutathSH+2H2O |
-0.2841 |
-0.3462 |
0.1841 |
0.28715 |
0.27604 |
Srhb+2H3O+ +2e-=HSH+2H2O
University
Alberta |
-0.2859 |
-0.3480 |
0.1739 |
0.27693 |
0.27424 |
Cytochrome c Fe3+ + e- = Fe2+ |
0.2442 |
0.2442 |
0.254 |
0.254 |
0.2442 |
LipoicAcidS-S+2H3O++2e-=LipSHSH+2H2O |
-0.3417 |
-0.4039 |
0.1241 |
0.22715 |
0.21837 |
Cytochrome c1 Fe3+ + e- = Fe2+ |
0.2115 |
0..2115 |
0.220 |
0.220 |
0.2115 |
AcetoAcetate-+2H3O+ +2e-=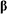 -OHButyrate-+2H2O -OHButyrate-+2H2O |
-0.3956 |
-0.4577 |
0.0681 |
0.17115 |
0.16453 |
 -Ketoglutarate2-+CO2+2H3O++2e-=isocitrate2-+2H2O -Ketoglutarate2-+CO2+2H3O++2e-=isocitrate2-+2H2O
|
-0.4283 |
-0.4904 |
0.0341 |
0.13715 |
0.13185 |
H3O++
e-=H(Pt) + H2O |
-0.4611 |
-0.5232 |
0.000 |
0.10303 |
0.09904 |
Cytochrome b Fe3+ + e- = Fe2+ |
0.074 |
0.074 |
0.077 |
0.077 |
0.074 |
CH3COOH+2H3O++2e-=CH3CHO+3H2OSuchotina |
-0.5784 |
-0.6407 |
-0.118 |
0.03654 |
0.03513 |
13PGlycerate4-+2H3O++2e-=Glycaldeh3-P2-+2H2O+Pi2- |
-0.5873 |
-0.6496 |
-0.1314 |
-0.0284 |
-0.0273 |
NADP++H3O+ +2e-=NADPH+ H2O |
-0.3429 |
-0.3740 |
-0.117 |
-0.0654 |
-0.0629 |
NAD+ +H3O+ +2e-=NADH + H2O David Harris |
-0.3391 |
-0.3702 |
-0.113 |
-0.0614 |
-0.0590 |
O2g+ e-
= O-2aq Suchotina |
-0.2355 |
-0.2355 |
-0.245 |
-0.245 |
-0.2355 |
Ferredoxin Fe3+ + e- = ferredoxin Fe2+ |
-0.415 |
-0.415 |
-0.432 |
-0.432 |
-0.415 |
2C3H4O3 + 4 H3O+ + 4e- = C6H12O6 + 4 H2O Stryer |
-.9975 |
-1.060 |
-0.5427 |
-0.4397 |
-0.4373 |
H2O + e- = H(Pt) + OH- Suchotina |
-0.5938 |
-0.6559 |
-0.828 |
-0.9311 |
-0.8951 |
Data mostly from: 1. Loach, P.A. (I 976) In Handbook of
Biochemistry and Molecular Biology,
2. 3rd edn (Fasman, G.D. ed.), Physical and Chemical Data,
Vol. 1, pp. 122-130 e, CRC Press,
3. A.M.Suchotina, Handbook of Electro-Chemistry,
Petersburg ,1981."Chimia"©
4. S.Kortly and L.Shucha. Handbook of
chemical equilibria in analytical chemistry. 1985.Ellis Horwood Ltd.©
5. University Alberta Data Tables Molar Thermodynamic
Properties of Pure Substances,
http://www.vhem.ualberta.ca/courses/plambeck/p101/p00403.htm
6.
Boca Raton,
FL.''This is the value for free FAD;
FAD bound to a specific flavo-protein
(for example succinate dehydrogenase) has a different E°
7. David A. Harris, "Bio-energetic at a Glance". b Blackwell Science Ltd ©, 1995, p.116.
8. Daniel C.Harris, "Quantitative chemical
analysis". W.H.Freeman and Company ©, 5th ed.1999, p545
E = E°+ 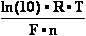 •lg
•lg
where E°- standard potential of given OxRed system measured at conditions when E=E° (as [Ox]=[Red]);
natural logarithm of number 10 - ln(10)=2.302585093 ; universal
gas constant - R=8.3144 J/mol/K ;
absolute thermodynamics temperature T=273.16°+ 25°(C)=298.16 K at standard temperature conditions measured:
as Kelvin scale value 273.16 K at zero 0°C point plus on Celsius
scale measured 25°C but human body temperature
37°C that will be higher T = 273.16° + 37°(C) = 310.16
K non-standard conditions;
Faraday's constant - F = 96 485 C (coulomb) 1 mol of
electrons e- electric
charge in C;
At 298 K (25°C) and at 310.16 K (37°C), this
expression reduces to respectively following expressions:
E = E°+
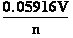 •lg
•lg ; E = E°+
; E = E°+ 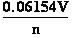 •lg
•lg
Many half-reactions of interest to biochemists involve protons H+or thermodynamically corrected
reality
hydronium ion H3O+. As in the
definition of  G°. biochemists define the standard state for oxidation-reduction
G°. biochemists define the standard state for oxidation-reduction
reactions as pH 7.36 and express the standard reduction potential as Eo, the standard reduction
potential at pH 7.36.
The standard reduction potentials given in Table 1 and used throughout
this book are values for Eo and are therefore
only valid for systems at neutral pH. Each value represents the
potential difference when the conjugate RedOx pair,
at equal concentrations [Ox]=[Red] and pH=7.36, is connected with the standard (pH=0) hydrogen electrode.
Notice in Table 1 that when the conjugate pair H+/H at pH 7 is connected with the standard hydrogen electrode
(pH 0), electrons e- tend to flow from the pH 7 cell => to => the standard (pH
0) cell; the measured Eo for the
H+/ H pair
according (3) is -0.05916*7=-
0.41412 V
Standard Reduction
Potentials Can Be Used to Calculate the Free-Energy Change
The usefulness of reduction
potentials stems from the fact that when reduction potentials E1 and E2 values have
been determined for any two 2 half-cells, relative to the standard
hydrogen electrode potential E°=0.00 V as
reference, their EMF=EOx2-ERed1 values relative to each other are also known. 'We can then predict the direction
Red1=> Ox2 in which electrons e- will tend => to
flow when the two 2 half-cells are connected through an
external circuit or when components Red1=> Ox2 of both half-cells are present in the same solution. Electrons e-
tend => to
flow to the half-cell with the more positive E° and the strength
of that tendency is proportional to the
difference in reduction potentials,  E°.
E°.
The energy  G made available by
this spontaneous electron e- flow => by work action
G made available by
this spontaneous electron e- flow => by work action  G = W
G = W
(the free-energy change  G for the oxidation-reduction reaction) is proportional ~ to
G for the oxidation-reduction reaction) is proportional ~ to  E. According RedOx system
E. According RedOx system
positive charged oxidized form Oxn+ - formed with lost electrons ne- - flows => from metal site (mostly used
platinum Pt and bearing free electron ne- gas) to
solution. In this movement process RedOx system are
accomplished the chemical work W = E•F•n by spending given RedOx system free energy
- G = -(GOx - GRed)
in conversion of reduced form Red to oxidized form Oxn+:
G = -(GOx - GRed)
in conversion of reduced form Red to oxidized form Oxn+:
Red  Oxn+ + ne-; W =
E•F•n =
Oxn+ + ne-; W =
E•F•n =  G (4)
G (4)
Here n represents the number of
electrons ne- transferred in the reaction.
Chemical
Potential of Species µ
Professor Ilya Prigogine and co
has shown that chemical potentialµ of compound A show,
how much change
of free energy  GA brings into system of our interest
when adding of 1 mol amount of compound A .
GA brings into system of our interest
when adding of 1 mol amount of compound A .
In a fact: how great amount of free energy belongs to one 1
mol of compound.
It means how much free energy  GA has itself per 1 mol compound A ,
GA has itself per 1 mol compound A ,
– chemical potential µ of compound A if amount of compound in
molar numbers is  nA = 1 mol
nA = 1 mol
µA = 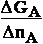 ; µA =
; µA =  G°
+ R•T•ln(XA) , (5)
G°
+ R•T•ln(XA) , (5)
where XA is concentration
of A unitles mol fraction XA = 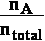
For pure compound A when nA = ntotal mol fraction is XA = 1 so ln(1)
= 0 and µ =  G° that
present
G° that
present
standard free energy of formation the 1 mol compound A from elements.
Reaction proceeds completely until end
only when products of reaction have hardly little disposition to reverse change
back. In other words these products of reaction have trifling or zero
value of chemical potential.
Data from:
I. Prigogine, R.
Defey. "Chemical Thermodynamics". 1954, Longmans Green and co ©.
Conditions of chemical equilibrium.
Provided chemical potential of
reaction products is taking into consideration (it has anything remarkable
level
of value), then reaction proceeds not completely until end, go not on but one
can observe the setting in equilibria.
In state of equilibria sum of chemical potentials for initial
compounds is equal to sum of chemical potentials
for products – according chemical equation
Red
 Oxn+ + ne- ; W = E•F•n =
Oxn+ + ne- ; W = E•F•n =  G
G
initial compounds products
work accomplished by movement
of positively (n+) charged Oxn+
form from metal surface, comprising electron ne- gas , and
touching Red form, to solution of RedOx system.
For RedOx system due to
electric work of charged Oxn+ movement between metal and RedOx system solution
sides are not equal µRed ≠ µOxn+ + n µe- but coefficient ne- means e-+e-+e-…n times electron e- takes a part
in reaction as is seen in expression of equilibrium (4). Free energy
change  G for
any chemical reaction is
G for
any chemical reaction is
to calculate as chemical potential sum subtraction: the product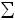 µproduct minus initial
µproduct minus initial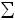 µinitial :
µinitial :
 G
= (
G
= (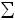 µOxn+ + n µe- ) -
µOxn+ + n µe- ) - 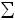 µRed=E•F•n , and equilibrium establishes when electric work is compensated
µRed=E•F•n , and equilibrium establishes when electric work is compensated
by free energy change  G=W=E•F•n and formation on metal (Pt) electrode
reduction potential E .
G=W=E•F•n and formation on metal (Pt) electrode
reduction potential E .
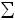 µRed+ E•F•n=
µRed+ E•F•n= 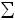 µOxn+ + nµe- (6)
µOxn+ + nµe- (6)
At equilibrium the chemical potential sum of initial compounds and products are equal
and reduced form includes
the compensating free energy change  G=W=E•F•n forming on metal (Pt) electrode
reduction potential E .
G=W=E•F•n forming on metal (Pt) electrode
reduction potential E .
Becomes obvious that chemical potential sum of oxidised form has
the number n additional chemical potential
of free electrons nµe- those values for all known RedOx systems are different and mostly laying
in side interval
between -90 ÷ +90 kJ/mol. Electrons ne- are
occupied metal (Pt) free electron gas solid phase and as pure solid
compound has mol fraction concentration Xe- = 1. Expressing above mentioned meaning of chemical
potentials (5)
we can calculate the free energy change  G in given RedOx system for Red form:
G in given RedOx system for Red form:
 G°Red + R•T•ln(XRed) + E•F•n=
G°Red + R•T•ln(XRed) + E•F•n=  G°Oxn+ + R•T•ln(XOxn+) + n
G°Oxn+ + R•T•ln(XOxn+) + n  G°e- + n•R•T•ln(Xe-)
G°e- + n•R•T•ln(Xe-)
 G°Red + R•T•ln(XRed) + E•F•n=
G°Red + R•T•ln(XRed) + E•F•n=  G°Oxn+ + R•T•ln(XOxn+) + n
G°Oxn+ + R•T•ln(XOxn+) + n  G°e- (7)
G°e- (7)
 G =
E•F•n =
G =
E•F•n =  G°Oxn+ +n
G°Oxn+ +n  G°e- -
G°e- -  G°Red + R•T•ln
G°Red + R•T•ln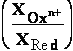
 G°
= E°•F•n =
G°
= E°•F•n =  G°Oxn+ +n
G°Oxn+ +n  G°e- -
G°e- -  G°Red (8)
G°Red (8)
Standard free energy change RedOx system for reduced form Red is expressed as  G°Red=E°•F•n and
G°Red=E°•F•n and
for oxidized form Oxn+ as  G°Oxn+ = - E°•F•n
G°Oxn+ = - E°•F•n
 GRed = E•F•n =
E°•F•n + R•T•ln
GRed = E•F•n =
E°•F•n + R•T•ln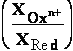 ;
;  GOxn+ = -E•F•n = -E°•F•n -
R•T•ln
GOxn+ = -E•F•n = -E°•F•n -
R•T•ln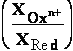 (9)
(9)
With this equation we can calculate the standardfree-energy change  G° for
any RedOx system from the values
G° for
any RedOx system from the values
of E° in a table of reduction potentials (Table 1) and the free-energy change  G according (9) at known
G according (9) at known
concentrations XRedand XOxn+ of the each species form ( GRed and
GRed and  GOxn+) participating in the RedOx system.
GOxn+) participating in the RedOx system.
Considerable oxidation-reduction reaction is composed from two 2RedOx systems (half-reactions)
using
compounds reaction equivalence law |+m'•ne-| = |-n'•me-|
we have balanced oxidation-redaction reaction and
can get the summary reaction of both half-reactions :
(-) Red1  Ox1n++ ne- |•m'
Ox1n++ ne- |•m'
(+) Ox2m+ + me- Red2 |•n'
Red2 |•n'
m'•Red1 + n'•Ox2m+=>m'•Ox1n++ n'•Red2 ; initial compounds => forming => products direction
of reaction.
With this equation we can calculate the standardfree-energy change  G° for equi-molar amount of any
G° for equi-molar amount of any
oxidation-reduction reaction from the values of E° in a table of
reduction potentials (Table 1)
 G° = m'•
G° = m'• G°1Red - n'•
G°1Red - n'• G°2Oxn+ = m'•E°1Red•F•n
- n'•E°2Oxn+•F•m = (E°1Red -E°2Oxn+)•F•(m'n=n'm), where nm
G°2Oxn+ = m'•E°1Red•F•n
- n'•E°2Oxn+•F•m = (E°1Red -E°2Oxn+)•F•(m'n=n'm), where nm
is equivalent - common number of electrons e- involved in RedOx reaction can be less n'm' ≤ n•m .
and the free-energy change  G according (9) at
known concentrations XRedand XOxn+ of the each species
G according (9) at
known concentrations XRedand XOxn+ of the each species
( GRed and
GRed and  GOxn+) participating in the reaction.
GOxn+) participating in the reaction.
 G=m'•
G=m'• G1Red-n'•
G1Red-n'• G2Oxn+=m'•E1Red•F•n
-n'•E2Oxn+•F•m =(E1Red-E2Oxn+)•F•(m'n=n'm)=
G2Oxn+=m'•E1Red•F•n
-n'•E2Oxn+•F•m =(E1Red-E2Oxn+)•F•(m'n=n'm)=
= (E°1Red-E°2Oxn+)•F•(m'n=n'm)+R•T•ln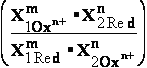 , where
equilibrium (10)
, where
equilibrium (10)
constant Keq = 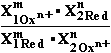 is the ratio as a multiple products over initial compounds concentrations.
is the ratio as a multiple products over initial compounds concentrations.
Consider the reaction in which acet-aldehyde is reduced by the biological electron carrier NADH:
H3C-CH=O + NADH + H3O+ H3C-CH2-OH + NAD+ + H2O (11)
H3C-CH2-OH + NAD+ + H2O (11)
acet-aldehyde ethanol
The relevant half-reactions and their E37 values at pH = 7.36 , (pH-log(1/aHOH)) are:
(1) NADH
+ H2O  NAD+ + H3O+ + 2e- E137 = -0.0590 V (David Harris)
NAD+ + H3O+ + 2e- E137 = -0.0590 V (David Harris)
(2) CH3CHO+2H3O+ + 2e-  CH3CH2OH+ 2 H2O E237 = 0.28169 V (Suchotina)
CH3CH2OH+ 2 H2O E237 = 0.28169 V (Suchotina)
By convention (10), n=2=m number of
electrons 2e-  E37 is expressed as E137 of the electron donor minus E237
E37 is expressed as E137 of the electron donor minus E237
of the electron acceptor. Because acet-aldehyde is accepting electrons from NADH in our example
 E37 = E137-E237 = -0.0590 V- 0.28169 V = -0.34069 V, and n is 2. Therefore -0.0590- 0.28625 -0.34525*2*96485 =
-66622.89250/1000 = -66.62289 kJ/mol
E37 = E137-E237 = -0.0590 V- 0.28169 V = -0.34069 V, and n is 2. Therefore -0.0590- 0.28625 -0.34525*2*96485 =
-66622.89250/1000 = -66.62289 kJ/mol
 G°
=
G°
=  E37•F•n
= -0.34069 V • 2 mol • 96485 C/mol = -65.7429495kJ/mol
E37•F•n
= -0.34069 V • 2 mol • 96485 C/mol = -65.7429495kJ/mol
This is the free-energy change for the oxidation-reduction reaction at equilibrium state when  G = 0 and so :
G = 0 and so :
 G°=
-R•T•ln(Keq);
G°=
-R•T•ln(Keq);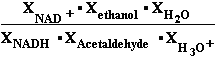 =Keq=
=Keq=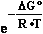 =
=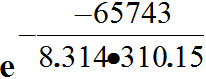 = 1.18065•1011
= 1.18065•1011
equilibrium is shifted far to products as shows Equilibrium constant Keq=1.181•1011. Anaerobic fermentation conditions NAD+ concentration exceeds NADH ratio 70 times at pH = 7.36. At presence of air oxygen O2 ratio [NAD+]/[NADH] is ten times higher 700 times over concentration NADH, what cause reaction condition to oxidize ethanol and acet-aldehyde as well known aerobic fermentation forms acetic acid. If ethanol ratio of concentrations is one as produced
ethanolequal the same acet-aldehyde amount in aerobic fermentation:
than calculated free energy change is positive
 G=5195 J/mol=(-65.7429495+70.938)27.51•8.3144•310.15• ln(8.85352•1011•1);
G=5195 J/mol=(-65.7429495+70.938)27.51•8.3144•310.15• ln(8.85352•1011•1);
 G= -742 J/mol=(-65.7429495+65.00071)25.21•8.3144•310.15• ln(8.85352•1011•0.1)
G= -742 J/mol=(-65.7429495+65.00071)25.21•8.3144•310.15• ln(8.85352•1011•0.1)
produces 10% ethanol over acetaldehyde and reaction shifted toward acetic acid:
Anaerobic  G shifted to ethanol negative:
G shifted to ethanol negative:
 G
= (E1Red -E2Oxn+)•F•(m'n=n'm) + R•T•ln
G
= (E1Red -E2Oxn+)•F•(m'n=n'm) + R•T•ln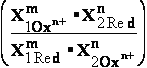
 G = (E°NADH - E°Acetaldehyde)•F•2 + R•T•ln
G = (E°NADH - E°Acetaldehyde)•F•2 + R•T•ln
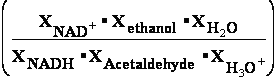
 G= -65.7429495 +8.3144•310.15•ln (8.85352•1010•0.1)
G= -65.7429495 +8.3144•310.15•ln (8.85352•1010•0.1)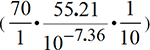 = -6680 J/mol
= -6680 J/mol
= -66.62289kJ/mol
+ 8.3144•310.16•ln(1.31368) =
-66.62289*1000+703.574102 = -66622.89000+703.574102 =-65919.315898/= -65.7429495kJ/mol+ 8.3144•310.16•ln(8.85352•1010•0.1) = -65.7429495+59.063= -6.680
Calculation the free-energy changes  G show possible modulation biological RedOx reaction at any
G show possible modulation biological RedOx reaction at any
concentrations X for the reaction driving forces and as regulation direction for favorable products formation.
BioThermodynamics.doc page 13 erythrocyte -53.47kJ/mol T=310,16 K .
Cellular
Oxidation of Glucose to Carbon Dioxide Requires Specialized Electron Carriers
The principles of oxidation-reductionenergetic described above apply to the many metabolic reactions
that
involve electron e- transfers. For example, in many organisms, the oxidation of glucose supplies energy for the
production of ATP. The complete oxidation of glucose: C6H12O6 + 6 O2==> 6 CO2 + 6 H2O
has a  G° of -3049,55 kJ/mol. This is a much larger release of free energy than is required for ATP synthesis
G° of -3049,55 kJ/mol. This is a much larger release of free energy than is required for ATP synthesis
(erythrocyte pH = 7.36 use -53.47kJ/mol 55,4% of 100% 120 kJ/mol. Cells do not convert glucose
to CO2aqua in a single, high-energy-releasing reaction, but rather in a
series of controlled reactions, some of which are
oxidations. The free energy released in these oxidation steps is of the same order of magnitude as that required for
ATP synthesis from ADP, with some energy to spare.
Electrons e- removed in these oxidation steps are transferred
to coenzymes specialized for carrying electrons e-,
such as NADH and FADH2 (described below).
A Few Types of Coenzymes
and Proteins Serve as Universal Electron Carriers
The multitude of enzymes that catalyze cellular oxidationschannel electrons e- from their hundreds 100 of different
substrates into just a few types of universal electron
carriers. The reduction of these carriers in catabolic processes
results in the conservation of free energy released by substrateoxidation. NAD+, NADP+, FMN, and FAD are
water-soluble coenzymes that undergo reversible  oxidation and reduction in many of the
electron-transfer e-
oxidation and reduction in many of the
electron-transfer e-
reactions of metabolism. The nucleotides NAD+ and NADP+ move readily from one enzyme to => another; the flavin
nucleotides FMN and FAD are usually very tightly bound to the enzymes, called flavo-proteins, for which they
serve as prosthetic groups. Lipid-soluble quinones such
as ubiquinone and plasto-quinone act as electron carriers
and protondonors in the non-aqueous environment of membranes. Iron-sulfur proteins and cytochromes, which
have tightly bound prosthetic groups that undergo reversible  oxidation and reduction,
also serve as electron e-
oxidation and reduction,
also serve as electron e-
carriers in many oxidation-reduction reactions. Some of these proteins are water-soluble, but others are peripheral
or integral membrane proteins.
We conclude this chapter by
describing some chemical features of nucleotide coenzymes and some of
the enzymes
(dehydrogenases and flavo-proteins) that use them. The oxidation-
reduction chemistry of quinones, iron-sulfur
proteins, and cytochromes is discussed in Oxidative
Phosphorylation and Photo-Phosphorylation.
NADH
and NADPH Act with Dehydrogenases as Soluble Electron Carriers
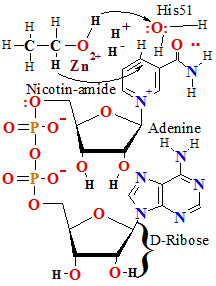
Nicotin-amide adenine
dinucleotide (NAD+ in its oxidized form) and its close analog nicotin-amide adenine
dinucleotidephosphate (NADP+) are composed of two 2nucleotides joined through their phosphate groups by
a phospho-anhydride bond (Fig. 3). Because the nicotinamide ring
resembles pyridine, these compounds are
sometimes called pyridinenucleotides. The vitamin niacin is the source of the nicotin-amide moiety in
nicotin-amide nucleotides.
Both coenzymes undergo
reversible  reduction of
the nicotinamide ring (Fig. 3). As a substrate molecule
reduction of
the nicotinamide ring (Fig. 3). As a substrate molecule
undergoes oxidation (dehydrogenation), giving up two 2 hydrogen H atoms, the oxidized form of the nucleotide
(NAD+ or NADP+) accepts a hydride ion (:H- the equivalent of a proton H+ and two 2 electrons e-)
and is
transformed into the reduced form (NADH or NADPH). The
second 2nd proton H+ removed from the substrate is
released to the aqueous solvent H2O. The half-reaction for each type of nucleotide is therefore
(1) NADH + H2O NAD+ + H3O+ + 2e- E137 = -0.0590 V (David Harris)
NAD+ + H3O+ + 2e- E137 = -0.0590 V (David Harris)
(2) NADPH + H2O NADP+ +
H3O+ + 2e- E237 = -0.0629 V (CRC)
NADP+ +
H3O+ + 2e- E237 = -0.0629 V (CRC)
Reduction of NAD+ or NADP+ converts the benzenoidring of the nicotin-amide moiety (with a fixed positive (+)
charge on the ring nitrogen N) to the quinonoid form (with no charge ° on the nitrogen
°N). Note that the reduced
nucleotides absorb light at 340 nm: the oxidized forms do
not (Fig. 13). The plus sign in the abbreviations NAD+ and
NADP+ does not
indicate the no charge on these molecules (they are both negatively (-)
charged), but rather that
the nicotin-amide ring is in its oxidized form, with a positive (+)
charge on the nitrogen N+ atom. In the abbreviations
NADH and NADPH, the "H" denotes the added hydride ion. To refer to these nucleotides without specifying their
oxidation state, we use NAD and NADP.
The total concentration of NAD++ NADH in most tissues is
about 10-5M; that of NADP+ + NADPH is about
10 times lower |¬.
In many cells and tissues, the ratio of NAD+ (oxidized)
to NADH (reduced) is high, favoring
hydride H- transfer from a substrate to NAD+ to form NADH. By contrast, NADPH (reduced) is generally present
in greater amounts
than its oxidized form, NADP+,
favoring hydride H- transfer from NADPH to a substrate.
This reflects the specialized metabolic roles of the two 2coenzymes: NAD+ generally
functions in oxidations - usually
as part of a catabolic reaction; and NADPH is the usual coenzyme
in reductions nearly always as part of anabolic
reaction. A few enzymes can use either coenzyme. but most show a strong preference for one over the other.
This functional specialization allows a cell to maintain two 2 distinct
pools of electron carrier, with two 2 distinct
functions, in the same cellular compartment.
More than 200 enzymes are known to
catalyze reactions in which NAD+ (or NADP+) accepts a hydride :H- ion
from a reduced substrate AH2,
or NADPH (or NADH) donates a hydride :H- ion to an oxidized substrate A.
The general reactions are
Red substrate AH2 + NAD+ + H2O A + NADH + H3O+ (11)
A + NADH + H3O+ (11)
Ox substrate A + NADPH + H3O+ AH2 + NADP+ + H2O (11)
AH2 + NADP+ + H2O (11)
where AH2is the reduced substrate and A the oxidized substrate. The general name for an enzyme of this type is
oxidoreductase; they are also commonly called dehydrogenases. For
example, alcohol dehydrogenase catalyzes
the first 1st step in the catabolism of ethanol, in which ethanol is oxidized to acet-aldehyde:
H3C-CH2-OH
+ NAD+ + H2O H3C-CH=O + NADH + H3O+ (11)
H3C-CH=O + NADH + H3O+ (11)
Ethanol Acet-aldehyde
Notice that one of the carbon atoms C in ethanol has lost a hydrogen H; the compound has been oxidized from
an alcohol to an aldehyde (Fig. 1).
When NAD+ or NADP+is reduced. the hydride :H- ion could in principle the transferred to either
side of
the nicotin-amide ring: the front (A side) or the back (B side) as represented in Figure 3. Studies with isotopically
labeled * substrates have shown that a given enzyme catalyzes
either an A-type or B-type transfer, but not both.
For example, yeast alcohol dehydrogenase and lactate
dehydrogenase of vertebrate heart transfer a hydride
:H- ion to (or remove a hydride :H- ion
from) the A side of the nicotin-amide ring: they are classed as
type A
dehydrogenases to distinguish them from another group of enzymes that
transfer a hydride :H- ion to
(or remove a hydride : H- ion from) the B side of the nicotin-amide
ring (Table 2).
The association between a dehydrogenase and NAD or NADP is relatively loose; the coenzyme readily
diffuses
from one enzyme to another, acting as a water-soluble carrier of electrons e- from one 1 metabolite to
another.
For example, in the production of alcohol during fermentation of glucose by, yeast cells, a hydride :H- ion is removed
from glycer-aldehyde 3-phosphate by, one 1 enzyme (glycer-aldehyde
3-phosphate dehydrogenase, a type B enzyme)
and transferred to NAD+.
The NADH produced then leaves the enzyme surface and
diffuses to another enzyme
(alcohol dehydrogenase, a type A enzyme), which transfers a hydride :H- ion to acet-aldehyde,
producing ethanol. Reduced (calculated) At T=310 K (37° C) human glyceraldehyde3phosphate:
Reduced (calculated)
OHC-CHOH-CH2OPO3H-+2H2O+HPO42- -2O3POOC-CHOHCH2OPO3H-+2e-+2H3O+E1=-0.0273V
-2O3POOC-CHOHCH2OPO3H-+2e-+2H3O+E1=-0.0273V
(Ox) NAD+ + H3O+ + 2e-  NADH + H2O E2H2O= -0.0614 V (David Harris)
NADH + H2O E2H2O= -0.0614 V (David Harris)
E137 = 0.0317 V + E2o = 0.0317 -0.059= -0.0273
glyceraldehyde3phosphate <=>1,3-PhosphoGlycerate
?G° = 6.117 kJ/mol = F•2•(E1o - E2o) ; (E1o - E2o) = ?G° /2/F = 6.117*1000/2/96485 = 0.0317 V
(1) OHC-CHOH-CH2OPO3H- + NAD+ + H2O + HPO42-=>
Glyceraldehyde 3-phosphate =>-2O3POOC-CHOHCH2OPO3H-+NADH+H3O+ G°=6.276 kJ/mol acetaldehyde 3-phospho-glycerate (Carnegie
Mellon Univ.)
G°=6.276 kJ/mol acetaldehyde 3-phospho-glycerate (Carnegie
Mellon Univ.)
(2) H3C-CH=O+NADH+H3O+ H3C-CH2-OH + NAD+ + H2O
H3C-CH2-OH + NAD+ + H2O  G°=
-58.856 kJ/mol (calculated)
G°=
-58.856 kJ/mol (calculated)
DG° =
6.276 kJ/mol = F•2•(E1o - E2o) ; (-0.113-0.192)•96485•2 = -0.305*2*96485/1000 =
-58.856+6.276
Sum H3CCHO+OHCCHOHCH2OPO3H-+H2O+HPO42-=>H3CCH2OH+-2O3POOCCHOHCH2OPO3H-
Sum  G° = 6.276
kJ/mol + -58.856 kJ/mol = -52.580 kJ/mol
G° = 6.276
kJ/mol + -58.856 kJ/mol = -52.580 kJ/mol
Notice that in the overall reaction there is no
net production or consumption of NAD+ or NADH; the coenzymes
function catalytically and are recycled repeatedly without a net change in the
concentration C of
[NAD+]+[NADH].
 + 2e- + H+=>
+ 2e- + H+=>
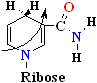 or=>
or=> 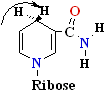
(a) NAD+ oxidized A side
NADH reduced B side
In NADP+ is  esterified this hydroxyl with phosphate
esterified this hydroxyl with phosphate
Absorbance

220
240
260
280
300
320
340
360
380 => nm
(b) Wavelength (nm)
=>
Figure 3.NAD and NADP (a) Nicotin-amide adenine
di-nucleotide (NAD+)
and its phosphorylated analog
NADP+ undergoes reduction to NADH and NADPH, accepting a hydride :H- ion (two 2 electrons e- and
one 1 proton H+)
from an oxidizablesubstrate. The hydride :H- ion is added to either the front (the A side) or
the back (the B side) of the planar nicotin-amide ring (see
Table 2). (b) The UV absorption spectra of NAD+ and
NADH. Reduction of the nicotin-amide ring produces a new,
broad absorption band with a maximum at 340 nm.
The production of NADH during an enzyme-catalyzed reaction can be
conveniently followed by observing
the appearance of the absorbance at 340 nm; a=6200M-1•cm-1
Table 2. Stereo specificity of Dehydrogenases That Employ NAD+ or NADP+ as Coenzymes
Enzyme |
Coenzyme |
Stereo chemical specificity for nicotin-amide
ring (A or B) |
Iso-citrate dehydrogenase |
NAD+ |
A |
a-Keto-glutarate dehydrogenase |
NAD+ |
B |
Glucose 6-phosphate dehydrogenase |
NADP+ |
B |
Malate dehydrogenase |
NAD+ |
A |
Glutamate dehydrogenase |
NAD+ |
or NADP+
B |
Glyceraldehyde 3-phosphate dehydrogenase |
NAD+ |
B |
Lactate dehydrogenase |
NAD+ |
A |
Alcohol dehydrogenase |
NAD+ |
A |
Table 3. Some Enzymes (Flavo-proteins) That Employ Flavin
Nucleotide Coenzymes
Enzyme |
Flavin nucleotide |
Fatty acyl-CoA dehydrogenase |
FAD |
Di-hydro-lipoyl dehydrogenase |
FAD |
Succinate dehydrogenase |
FAD |
Glycerol 3-phosphate dehydrogenase |
FAD |
Thio-redoxin reductase |
FAD |
NADH dehydrogenase (Complex 1) |
FMN |
Glycolate dehydrogenase |
FMN |
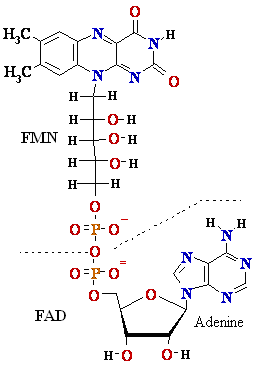
|¬ flavin mono-nucleotide (FMN)
isoalloxazine ring
 +e-+H+
+e-+H+
 +e-+H+
+e-+H+
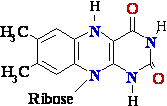
Flavin adenine dinucleotide (FAD)
=> FADH* (FMNH*) => FADH2 (FMNH2)
=> (FMN) (semi-quinone)=> (fully reduced)
Figure
4. Structures of oxidized and reduced
FAD and FMN. FMN consists of the structure above the
dashed line
shown on the oxidized (FAD) structure.
The flavin nucleotides accept two 2 hydrogen H atoms (two 2 electrons e-
and two 2 protons H+),
both of which appear in the flavin ring system. When FAD or FMN
accepts only
one 1 hydrogen H atom, the semi-quinone,
a stable free radical, forms.
Flavin
Nucleotides Are Tightly Bound in Flavo-proteins
Flavo-proteins (Table 3)
are enzymes that catalyze oxidation-reduction reactions
using either flavin
mono-nucleotide (FMN) or flavin adenine dinucleotide (FAD)
as coenzyme (Fig. 4). These coenzymes are
derived from the vitamin riboflavin. The fused ring structure of flavin nucleotides (the isoalloxazine ring)
undergoes reversible reduction, accepting either one 1 or two 2 electrons e- in the form of one 1 or two 2 hydrogen H
atoms (each atom an electron e- plus a proton H+) from a reduced substrate.
The fully reduced forms are abbreviated
FADH2 and FMNH2. When a fully oxidizedflavin
nucleotide accepts only one 1 electron e- (one
hydrogen H atom),
the semi-quinone form of the isoalloxazine ring is produced,
abbreviated FADH* and FMNH*. Because
flavo-proteins can participate in either one-1 or two-2 electron e- transfers, this class of proteins is involved in
a greater diversity of reactions than the pyridine nucleotide-linked dehydrogenases.
Like the nicotin-amide
coenzymes (Fig. 14-15), the flavin nucleotides undergo a shift in a
major absorption band
on reduction. Oxidized flavo-proteins generally have an
absorption maximum near 570 nm; when reduced,
the absorption maximum shifts => to about 450 nm. This change can be used to assay reactions
involving
a flavo-protein.
The flavin nucleotide in
most flavo-proteins is bound rather tightly to the protein,
and in some enzymes, such
as succinate dehydrogenase, it is bound covalently. Such tightly
bound coenzymes are properly called prosthetic
groups. They do not transfer electrons e- by diffusing from
one 1enzyme to another second 2nd; rather, they provide
a means by which the flavo-protein can temporarily hold electrons e- while it catalyzes electron e- transfer from
a reducedsubstrate to an electron e- acceptor.
One important feature of the flavo-proteins is the variability in
the standard reduction potential (E°) of the bound flavin
nucleotide. Tight association between the enzyme and
prosthetic group confers on the flavin ring a reduction
potential E typical of that particular flavo-protein, sometimes
quite different from that of the free flavin nucleotide. FAD bound to succinate dehydrogenase, for example, has an
EM = 0.0953 V compared
with -0.3356 V for free FAD. Flavo-proteins are
often very complex: some have, in addition
to a flavin nucleotide. tightly bound inorganic
ions (iron Fen+ or molybdenum Mon+,
for example) capable
of participating in electron e- transfer.
Summary
Living cells constantly perform
work W and thus require energy E for the maintenance of highly
organized.
structures, for the synthesis or
cellular components, for movement, for the generation of electric
currents,
for the production of light, and for many other processes. Bio-energetic is the quantitative study of energy E
relationships and energy E conversions in biological systems. Biological energy E transformations obey the laws
of thermodynamics. All chemical reactions are influenced by two 2 forces: the tendency to achieve the most
stable bonding state (for which enthalpy, H, is a useful expression to
show minimum reach at the most stable
bonding state ) and the tendency to achieve the
highest^degree of dispersed energy, T•S (called bound energy),
which measure is the entropy, S. The production of entropy in a reaction
as positive difference  S
= Sproducts - Sreactants> 0
S
= Sproducts - Sreactants> 0
is entropy increase^from Sreactants to Sproducts due
to dispersion of energy among the members of reaction. The net
driving force in a reaction is the free-energy G decrease => from Greactants to=> Gproducts and negative difference
 G = Gproducts - Greactants< 0, which
represents the net effect of these
G = Gproducts - Greactants< 0, which
represents the net effect of these
two 2 factors: T• S+
S+ G =
G =  H . Cells require sources of free energy G to perform work W.
H . Cells require sources of free energy G to perform work W.
The standard transformed
free-energy change,  G°,
is a physical constant characteristic for a given reaction and
G°,
is a physical constant characteristic for a given reaction and
can be calculated from the equilibrium constant Keq for the reaction:  G°=
-R•T•In(Keq). The actual free-energy
G°=
-R•T•In(Keq). The actual free-energy
change,  G, is
a variable, which depends on,
G, is
a variable, which depends on,  G° and on the concentrations C of reactants and products:
G° and on the concentrations C of reactants and products:
 G=
G=  G°+
R•T•ln([products]/[reactants]).
When
G°+
R•T•ln([products]/[reactants]).
When  G is
large and negative
G is
large and negative  G
< 0, the reaction tends to go in
G
< 0, the reaction tends to go in
the forward => direction; when it is large and positive  G > 0, the reaction tends to go in the
reverse <= direction;
G > 0, the reaction tends to go in the
reverse <= direction;
and when  G = 0,
the system is at equilibrium. The free-energy change
G = 0,
the system is at equilibrium. The free-energy change  G for a reaction is
independent of
G for a reaction is
independent of
the pathway by which the reaction occurs only on initial(Greactants) and final (Gproducts) states. Free-energy
changes  G
G
are additive; the net chemical reaction that results from the successive
occurrence of reactions sharing a common
intermediate has an overall free-energy change  Greaction that is the sum of the
Greaction that is the sum of the  Greaction =
Greaction =  Greaction1 +
Greaction1 +  Greaction2 values
Greaction2 values
for the individual reactions reaction1 and reaction2.
ATP is the chemical link
between catabolism and anabolism. It constitutes the energy currency
of the living cell.
Its ex-ergonic conversion to ADP and Pi, or to AMP and PPi, is coupled to a large number of endergonic reactions
and processes. In general, it is not ATPhydrolysis, but the
transfer of a phosphoryl, pyro-phosphoryl, or adenylyl
group from ATP to a substrate or enzyme molecule that
couples the energy of ATP breakdown to endergonic
transformations of substrates. By these group transfer reactions, ATP provides the energy for anabolic reactions,
including the synthesis of informational molecules, and for the transport of molecules and ions across membranes
against <=> concentration C gradients and electrical potential E gradients.
Muscle contraction is one of several
exceptions to this generalization; the conformational changes that produce
muscle contraction are driven by ATP
hydrolysis directly.
Cells contain other metabolites with large, negative  G
< 0, free energies of hydrolysis, including
G
< 0, free energies of hydrolysis, including
phospho-enol-pyruvate, 1,3-bis-phospho-glycerate,
and phospho-creatine. These high-energy compounds,
like ATP, have a high phosphoryl group transfer potential;
they are good donors of the phosphoryl group.
Thio-esters also have high free energies G of hydrolysis.
Biological oxidation-reduction reactions can be described in terms of two 2 half-reactions (called RedOx systems),
each with a characteristic standard reduction potential, E°. When two 2 electro-chemical half-cells, each containing
the components (oxidized and reduced forms) of a half-reaction,
are connected, electrons e- tend to flow => to
the half-cell with the higher^reduction potential E. The strength
of this tendency is proportional to the difference
between the two 2reduction potentials ( E) and is a function of the
concentrations C of oxidized [Ox] and
E) and is a function of the
concentrations C of oxidized [Ox] and
reduced [Red] species. The standard free-energy change  G° for an oxidation-reduction reaction is directly
G° for an oxidation-reduction reaction is directly
proportional to the difference in standard reduction potentials  E° of the two 2 half-cells:
E° of the two 2 half-cells:  G°
= F•n•
G°
= F•n• E°.
E°.
Many biological oxidation reactions are dehydrogenation in which one 1 or two 2 hydrogen H atoms (electron e-
and proton H+)
are transferred from a substrate to a hydrogen Hacceptor. Oxidation-reduction reactions in cells
involve specialized electron e-carriers. NAD and NADP are the freely diffusible coenzymes of many
dehydrogenases. Both NAD+ and NADP+accept two 2 electrons e- and one 1 proton H+. FAD and FMN, the flavin
nucleotides, serve as tightly bound prosthetic groups of flavo-proteins.
They can accept either one 1 or
two 2 electrons e-. In many organisms, a central
energy-conserving process is the stepwiseoxidation of glucose
to CO2, in which some of the energy of oxidation is conserved in ATP as electrons e- are passed to O2.
Further
Reading
Bio-energetic and Thermodynamics
1.
Prigogine, R. Defey. "Chemical Thermodynamics". 1954, Longmans Green and co ©.
Correct basic concepts for Biochemical Thermodynamics.
2. S.Kortly
and L.Shucha. Handbook of chemical equilibria in
analytical chemistry.
1985.Ellis Horwood Ltd.©
3.
3rd edn (Fasman, G.D. ed.), Physical and Chemical Data, Vol. 1, pp.
130 e,
The Chemical Rubber Publishing Co. CRC Press ©
4. Atkins, P.W. (1984) The Second Law, Scientific
American Books, Inc.,
New York.
A well-illustrated and elementary discussion of the second
law and its implications.
5. Becker, W.M. (1977) Energy and the Living Cell: An Introduction to
Bio-energetics,
J.B. Lippincott Company,
Philadelphia.
A, clear introductory account of cellular metabolism, in
terms of energetics.
6. Bergethon, P.R. (1998) The Physical Basis of
Biochemistry, Springer Verlag,
New
York.
The excellent general references for physical biochemistry, with good
discussions of the
application of thermodynamics to biochemistry.
7. Edsall, J.T. & Gutfreund, H. (198.'3) Bio-thermodynamics: The Study
of Biochemical
Processes at Equilibrium, John Wiley & Sons, Inc.,
New York.
8. Harold, F.M. (1986) The Vital Force: A Study of Bio-energetics,
W.H. Freeman and Company,
New York.
A beautifully clear discussion of thermodynamics in
biological processes.
9. Harris, D.A. (1995) Bio-energetics at a Glance, Blackwell Science,
Oxford.
A short, clearly written account of cellular energetics,
including basic concepts on thermodynamics.
10. Morowitz, H.J. (1978) Foundations of Bio-energetics, Academic Press,
Inc.,
New York.
Clear, rigorous description of thermodynamics biology. Out of print.
11. Tinoco, L, Jr., Saner, K., & Wang, J.C. (1996)
Physical Chemistry: Principles and Applications in Biological Sciences,
3rd edn, Prentice-Ha1l, Inc.,
Upper
Saddle River,
NJ.
Thermodynamics.
12. van Holde, K.E., Johnson, W.C., & Ho, P.S. (1998) Principles of Physical Biochemistry,
Prentice-Hall, Inc.,
Upper Saddle
River
N.J.
Phosphoryl Group Transfers and ATP
1.
Alberty, R.A. (1994) Biochemical thermodynamics. Biochim. Biophys. Acta 1207, 1-11.
Explains the distinction between biochemical and chemical
equations, and the calculation and
meaning of transformed thermodynamic properties for ATP and other
phosphorylated compounds.
2.
Bridger, W.A. & Henderson, J.F. (1983) Co/I ATP, .John Wiley &
Sons, Inc.,
New York.
The chemistry of ATP, its role in metabolic regulation, and
its catabolic and anabolic roles.
3.
Frey, P.A. & Arabshahi, A. (1995) Standard
free-energy change for the hydrolysis of
the a-b-phospho-anhydride bridge
in ATP. Biochemistry 34, 1 1,307-11,310.
4.
Hanson, R.W. (1989) The role of ATP in metabolism. Biochem. Educ. 17, 86-92,
Excellent summary of the chemistry and biology of ATP
5.
Lipmann, F. (1941) Metabolic generation and utilization
of phosphate bond energy.
Adv. enzymol. 11,96-162.
The classic description of the role of high-energy phosphate compounds in
biology.
6.
Pullman, B. & Pullman,
A. (1960) Electronic structure of energy-rich phosphates.
Radiat. Res. Suppl. 2, pp. 160-181.
An advanced discussion of the chemistry of' ATP and other
''energy-rich'' compounds.
7.
Veech, R.L., Lawson, J.W.R., Cornell, N.W., & Krebs, H.A. (1979)
Cytosolic phosphorylation potential. J Biol. Chem. 254,
6538-6547.
Experimental determination of ATP, ADP and Pi concentrations
in brain, muscle, and liver, and
a discussion of the problems in determining the real free-energy change for ATP
synthesis in cells.
8.
Westheimer, F.H. (1987) Why nature chose
phosphates. Science 235, 1173-1178.
A chemist's description of the unique suitability of
phosphate esters and anhydrides
for metabolic transformations.
Biological Oxidation- Reduction Reactions
1.
Dolphin, D., Avramovic, O., & Poulson, R. (eds)
(1987) Pyridine Nucleotide Coenzymes:
Chemical, Biochemical, and Medical Aspects, John Wiley & Sons, Inc.,
New York.
An excellent two-volume collection of authoritative reviews. Among the most useful are
the problems by Kaplan, Westheimer, Veech, and Ohno and Ushio.
Problems
1. Entropy Changes during Egg Development
Consider a system consisting of an egg in an incubator. The white and yolk of the egg contain proteins,
carbohydrates, and lipids. If fertilized, the egg is transformed from a single meiotic cell to a complex mitotic cells
in organism. Discuss this irreversible => process in terms of the entropy changes  S in the system, surroundings,
S in the system, surroundings,
and universe. Be sure that you first clearly define the system and surroundings-environment.
2. Calculation of  G° from Equilibrium
Constants
G° from Equilibrium
Constants
Calculate the standard free-energy changes  G° the following metabolically
important enzyme-catalyzed reactions
G° the following metabolically
important enzyme-catalyzed reactions
at 25°C and pH 7.0 from the equilibrium constants Keq given.
(a)  G° = - R•T•ln(Keq)
= -8.3144*298.16•ln(6.8) = -2479.0215*1.916923=
-4752.093331 = -4.752 kJ/mol
G° = - R•T•ln(Keq)
= -8.3144*298.16•ln(6.8) = -2479.0215*1.916923=
-4752.093331 = -4.752 kJ/mol
Glutamate+oxalo-acetate<=> aspartate
amino-transferase <=> aspartate + 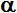 -keto-glutarate Keq=6.8
-keto-glutarate Keq=6.8
(b)  G°
= - R•T•ln(Keq) = -8.3144*298.16•ln(0.0475) = -2479.0215*-3.04703= 7553.65288 = 7.553 kJ/mol
G°
= - R•T•ln(Keq) = -8.3144*298.16•ln(0.0475) = -2479.0215*-3.04703= 7553.65288 = 7.553 kJ/mol
Di-hydroxy-acetone phosphate <=>triose
phosphate isomerase <=> glyceraldehyde 3-phosphate Keq= 0.0475
(c)  G°
= - R•T•ln(Keq) = -8.3144*298.16•ln(254) = -2479.0215*5.537334= -13727.170039 = -13.727 kJ/mol
G°
= - R•T•ln(Keq) = -8.3144*298.16•ln(254) = -2479.0215*5.537334= -13727.170039 = -13.727 kJ/mol
Fructose 6-phosphate- +ATP4-<=>phospho-fructo-kinase<=>fructose 1,6-bisphosphate2- + ADP3- Keq=254
 G°
= - R•T•ln(Keq) ;
G°
= - R•T•ln(Keq) ;  G =
G =  G° + R•T•ln(Keq)
G° + R•T•ln(Keq)
3. Calculation of Equilibrium Constants Keq from  G°
G°
Calculate the equilibrium constants Keq for each of the following
reactions at pH 7.0 and 25°C, using
the  G° values
of Table 1-1 Keq = EXP
G° values
of Table 1-1 Keq = EXP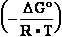 =
-13.8*1000/8.3144/298.16 = EXP(--5.5667) = 261.573 corrected
by DG° = -R•T•ln(K°eq) = -8.3144*298.16•ln(299.9981•10-7
=
-13.8*1000/8.3144/298.16 = EXP(--5.5667) = 261.573 corrected
by DG° = -R•T•ln(K°eq) = -8.3144*298.16•ln(299.9981•10-7
) = -2479.0215*-15.0195 = 37233.6634
 G°=
G°= G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O=
G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O=
= -13.8 + (-1282) + (-284.7) - (-1323) - (-306.7) = 49.306 kJ/mol
DG° = -R•T•ln(299.9981•10-9)=37.2336kJ/mol ; K°eq= 1.1469*261.573•10-9 = 299.9981•10- K°7eq=3;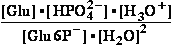 =3•10-7=K°H2PO4•Keq=1.15•10-9•261.573= K°eq;
=3•10-7=K°H2PO4•Keq=1.15•10-9•261.573= K°eq; G°eq= 37.2 kJ/mol
G°eq= 37.2 kJ/mol
H2PO4- + H2O<=>HPO42- + H3O+ ; K°H2PO4 = 1.1469•10-9 (Kortly Shucha)
(a) Glucose 6-phosphate-+H2O<=>glucose6-phosphatase<=>glucose+H2PO4-;Keq=261.573; G°o=-13.8 kJ/mol
G°o=-13.8 kJ/mol
Glucose 6-phosphate-+2H2O<=>glucose6-phosphatase<=>glucose+HPO42-+H3O+;K°eq=3•10-7; G°= 49.3 kJ/mol
G°= 49.3 kJ/mol
Equilibrium is shifted toward formation of
Glucose 6-phosphate- <= and is affected by H3O+ concentration.
(b) K°eq =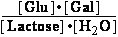 = 610.221 ;
= 610.221 ;  G° = -15.9 kJ/mol
G° = -15.9 kJ/mol
(b) Lactose + H2O <=>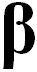 -galactosidase<=>glucose + galactose
KeqH2O = 33773
-galactosidase<=>glucose + galactose
KeqH2O = 33773
(c) Malate<=>fumarase<=>fumarate + H2O
KeqH2O = 0.004615
(c) K°eq =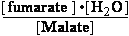 = 0.28636 ;
= 0.28636 ;  G° = 3.1 kJ/mol
G° = 3.1 kJ/mol
4. Experimental Determination of K°eq and  G°
G°
If a 0.1 M solution of glucose 1-phosphate is incubated
with a catalytic amount of phospho-gluco-mutase,
the glucose 1-phosphate is transformed to glucose 6-phosphate. At
equilibrium, the concentrations of
the reaction components are:
Glucose 1-phosphate-<=>phospho-gluco-mutase<=>glucose
6-phosphate-
[Glu6P-] = 4.5•10-3 M
9.6•10-2 M = [Glu6P-]
Calculate K°eq=[Glu6P-]/[Glu1P-]=21.3 and  G°=-R•T•ln(21.33)=-7.586
kJ/mol for this reaction at 25°C.
G°=-R•T•ln(21.33)=-7.586
kJ/mol for this reaction at 25°C.
5. Experimental Determination of  G° for ATP Hydrolysis
G° for ATP Hydrolysis
A direct measurement of the
standard free-energy change  G° associated with the hydrolysis of ATP is
G° associated with the hydrolysis of ATP is
technically demanding because the minute amount of ATP remaining at
equilibrium is difficult to measure
accurately. The value of  G° can be calculated indirectly, however, from the equilibrium constants of two 2
G° can be calculated indirectly, however, from the equilibrium constants of two 2
other enzymatic reactions having less favorable equilibrium constants:
 G°1=
G°1= G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O=49.306 kJ/mol
G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O=49.306 kJ/mol
H2PO4- + H2O<=>HPO42- + H3O+ ; K°H2PO4 = 1.1469•10-9 (Kortly Shucha)
Glucose-6-phosphate- + H2O => glucose + H2PO4- ; Keq= 270 ;  G°eq= -13.879 kJ/mol
G°eq= -13.879 kJ/mol
Glucose 6-phosphate- + H2O  glucose
+ H2PO4- ; K°o = 261.573 ;
glucose
+ H2PO4- ; K°o = 261.573 ;  G°o= -13.8 kJ/mol
G°o= -13.8 kJ/mol
K°eq•K°H2PO4=K°eq1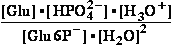 =3.1•10-7; = 4.7262•10-7 =
1.1469*261.573•10-9 =
=3.1•10-7; = 4.7262•10-7 =
1.1469*261.573•10-9 = G°eq1=37.16 kJ/mol
G°eq1=37.16 kJ/mol
(1) Glucose-6-phosphate- + 2 H2O => glucose + HPO42- + H3O+ ; K°eq1= 3.097•10-7; G°1=
49.3 kJ/mol
G°1=
49.3 kJ/mol
(2) ATP4- + glucose => ADP3- + glucose 6-phosphate- ; Keq2= 890
K°eq2 =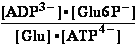 = 890 ;
= 890 ;  G°eq2=
-16.836 kJ/mol
G°eq2=
-16.836 kJ/mol
Using this information, calculate the standard
free energy  G° of hydrolysis of ATP at 25°C.
G° of hydrolysis of ATP at 25°C.
K°eq3=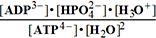 =K°eq1•K°eq2 =
=K°eq1•K°eq2 =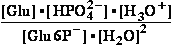 •
•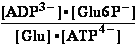
 G°3=
G°3= G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -30.5 + (-1282) + (-284.7) - (-1323) - (-306.7) = 32.606 kJ/mol
G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -30.5 + (-1282) + (-284.7) - (-1323) - (-306.7) = 32.606 kJ/mol
(3)ATP4-+2H2O=>ADP3-+HPO42-+H3O+; K°eq3=0.0002756; G°eq3=20.32 kJ/mol;
G°eq3=20.32 kJ/mol; G°123=32.464
kJ/mol
G°123=32.464
kJ/mol
Keq°o=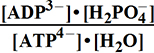 =K°eq3/K°H2PO4= 240300 ;
=K°eq3/K°H2PO4= 240300 ;  Geq°o = -30.714 kJ/mol
Geq°o = -30.714 kJ/mol
(3) ATP4- + H2O => ADP3- + H2PO4- ; K°o = 220409 ; G°o = -30.500 kJ/mol
G°o = -30.500 kJ/mol
6. Difference between  G° and
G° and  G Consider the following
inter conversion, which occurs in glycolysis :
G Consider the following
inter conversion, which occurs in glycolysis :
Fructose 6-phosphate-<=>glucose 6-phosphate- ; K°eq= 1.97
K°eq=
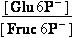 = 1.97 = 531 331 ;
= 1.97 = 531 331 ;  G°=
-R•T•ln(K°eq) = -1.5399 kJ/mol
G°=
-R•T•ln(K°eq) = -1.5399 kJ/mol
(a) What is  G° for the reaction (assuming that the temperature is 25°C)?
G° for the reaction (assuming that the temperature is 25°C)?
(b) If the concentration of [Fruc6P-] is
adjusted to 1.5 M and that of
[Glu6P-] is adjusted to 0.5 M, what is  G? -1539.9+R•T•ln(0.3)
=
G? -1539.9+R•T•ln(0.3)
=
(c) Why are  G° and
G° and  G different?
G different?  G=
G=  G° +
R•T•ln(
G° +
R•T•ln(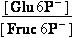 ) = -1539.9+-2723.54 =-4.263.4 kJ/mol
) = -1539.9+-2723.54 =-4.263.4 kJ/mol
7. Dependence of  G on pH. The free energy
G on pH. The free energy  G released by the hydrolysis of ATP under standard conditions
G released by the hydrolysis of ATP under standard conditions
at pH=7 is  G°o=-30.5 kJ/mol. If ATP is hydrolyzed under standard conditions but at pH=5.0, is more or less
G°o=-30.5 kJ/mol. If ATP is hydrolyzed under standard conditions but at pH=5.0, is more or less
free energy released? Why?
K°eq3=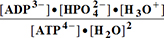 =1.94•10-6;K°eq3/K°H2PO4=K°o=
=1.94•10-6;K°eq3/K°H2PO4=K°o=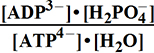 =220409
=220409
 G°3=
G°3= G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -30.5 + (-1282) + (-284.7) - (-1323) - (-306.7) = 32.606 kJ/mol
G°o+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -30.5 + (-1282) + (-284.7) - (-1323) - (-306.7) = 32.606 kJ/mol
 G=
G= G°+R•T•ln
G°+R•T•ln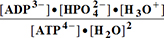 =32606+R•T•ln(0.0001/0.01/aoHOH/aoHOH*0.01•10-pH)== 19397.7 -7981.3= -10.11 kJ/mol (pH=0);
at T=25°C
=32606+R•T•ln(0.0001/0.01/aoHOH/aoHOH*0.01•10-pH)== 19397.7 -7981.3= -10.11 kJ/mol (pH=0);
at T=25°C
-38.65 kJ/mol (pH=5); -50.06 kJ/mol (pH=7); -52.12 kJ/mol (pH=7.36); -57.88 kJ/mol (pH=8.37)
-11.83 kJ/mol (pH=0); at T = 37°C in
mitochondria
-41.52 kJ/mol (pH=5); -53.39 kJ/mol (pH=7); -55.53 kJ/mol (pH=7.36); -61.53 kJ/mol (pH=8.37)
8. The  G° for Coupled Reactions
G° for Coupled Reactions
Glucose 1-phosphate- is converted into fructose 6-phosphate- in two 2 successive reactions:
Glucose 1-phosphate- => glucose 6-phosphate- ;  G°1 = -7.3 kJ/mol
G°1 = -7.3 kJ/mol
Glucose 6-phosphate- =>. fructose 6-phosphate-  G°2 = +1.7 kJ/mol
G°2 = +1.7 kJ/mol
Using the  G° values in Table 1.1, calculate the
equilibrium constant,
G° values in Table 1.1, calculate the
equilibrium constant,
 G°=
G°=  G°1+
G°1+ G°2 = -7.3+1.7
= -5.6 kJ/mol for the sum of the two 2 reactions at 25°C:
G°2 = -7.3+1.7
= -5.6 kJ/mol for the sum of the two 2 reactions at 25°C:
Glucose 1-phosphate- => fructose 6-phosphate- ; K°eq= Keq1•Keq2 = EXP(5600/8.314400/298.16) =
EXP(2.258956) = 9.57309
9. Strategy for Overcoming an Unfavorable
Reaction: ATP-Dependent Chemical CouplingThe
phosphorylation of glucose to glucose 6-phosphate- is the initial
step in the catabolism of glucose. The
direct phosphorylation of glucose by H2PO4- and HPO42- is described by the equation at T = 310.16 K:
(a) Glucose + H2PO4-=>. glucose 6-phosphate- + H2O,  Go°
=13.8 kJ/mol
Go°
=13.8 kJ/mol
K°a=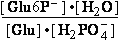 ; K°a2•K°H2PO4 =
; K°a2•K°H2PO4 =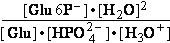 •
•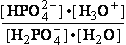
(a2) Glucose + HPO42- + H3O+ =>glucose 6-phosphate- + 2H2O,  G°=-49.306 kJ/mol
G°=-49.306 kJ/mol
K°a2=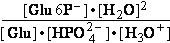 =
=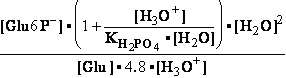 =2.0119•10+8
=2.0119•10+8
K°H2PO4=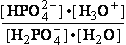 ; Pi=4.8 mM=[H2PO4-]+[HPO42-];[HPO42-]=4.8
-
; Pi=4.8 mM=[H2PO4-]+[HPO42-];[HPO42-]=4.8
- 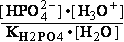 =
=
=[HPO42-]+[HPO42-]•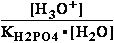 =4.8=[HPO42-]•(1+
=4.8=[HPO42-]•(1+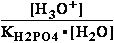 );
);
[HPO42-]=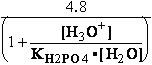 ; [Glu6P-]
=
; [Glu6P-]
=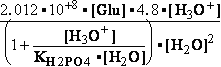 = 1.0574•10-5M
= 1.0574•10-5M
(a) Calculate the equilibrium constant K°a for the above
reaction. In the rat hepatocytepH=7.36 and at pH=7
the physiological concentrations of glucose and [H2PO4-]+[HPO42-]
are maintained at approximately 4.8 mM. What is
the equilibrium concentration of glucose 6-phosphate- obtained by the direct phosphorylation of glucose by
H2PO4-+HPO42-?
Respectively [Glu6P-] = 8.5•10-8M and 1.275•10-7M (pH 7.36 and 7)
Does this reaction represent a reasonable metabolic step for the catabolism of glucose? Explain.
(b) In principle, at least, one way to increase the
concentration of glucose 6-phosphate- is to drive the equilibrium
reaction to the right by increasing the intracellular concentrations of glucose and
H2PO4- + HPO42-. Assuming a fixed
concentration of H2PO4- + H2PO42- at 4.8 mM, how high would the
intracellular concentration of glucose have to be to give an equilibrium
concentration of glucose 6-phosphate-
of [Glu6P-]=250 µM (normal physiological
concentration)'? Would this route be physiologically reasonable, given
that the maximum solubility of glucose is less than 1 M?
[Glu]=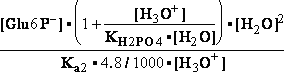 = 23.64M at pH=7.36 23.64259868
= 23.64M at pH=7.36 23.64259868
(c) The phosphorylation of glucose in the cell is coupled to the hydrolysis of ATP; that is, part of
the free energy
of ATP hydrolysis is utilized to effect the endergonic
phosphorylation of glucose at T = 310.16 K:
(1) Glucose + H2PO4-<=>glucose6-phosphate- + H2O
;  G°o1 = 13.8
kJ/mol
G°o1 = 13.8
kJ/mol
(2) ATP4- + H2O<=>ADP3- + H2PO4- ; K°o = 220409 ;  G°o2 = -30.500
kJ/mol
G°o2 = -30.500
kJ/mol
Sum: ATP4- + glucose<=>ADP3- + glucose 6-phosphate- ;  G°o =
-16.7 kJ/mol at To = 298.16 K
G°o =
-16.7 kJ/mol at To = 298.16 K
K°o= 842.63 <= EXP(- G°/R/T) = 649.3 = K°;
K°eqo=
G°/R/T) = 649.3 = K°;
K°eqo= 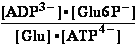 =890
;
=890
;  G°eqo=
-16.836 kJ/mol
G°eqo=
-16.836 kJ/mol
(1) glucose + HPO42-
+ H3O+<=>Glucose-6-phosphate- + 2H2O ; G°1 = -49.3 kJ/mol
G°1 = -49.3 kJ/mol
(2) ATP4-+2H2O<=>ADP3-+HPO42-+H3O+ ;  G°2= 32.606 kJ/mol
G°2= 32.606 kJ/mol
Sum: ATP4- + glucose<=>ADP3- + glucose 6-phosphate- ; G° =
-16.694 kJ/mol
G° =
-16.694 kJ/mol
 G°2=
G°2= G°o2+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -30.5 + (-1282) + (-284.7) - (-1323) - (-306.7) = 32.606 kJ/mol
G°o2+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -30.5 + (-1282) + (-284.7) - (-1323) - (-306.7) = 32.606 kJ/mol
[Glu]=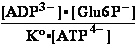 =
=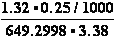 = 1.504•10-7M not depend on
concentration [H3O+]
= 1.504•10-7M not depend on
concentration [H3O+]
Calculate K for the overall reaction.
For the ATP-dependent phosphorylation of glucose, what
concentration of
glucose is needed to achieve a 250 µM intracellular concentration of
glucose 6-phosphate when the concentrations
of ATP and ADP are 3.38 and 1.32 mM, respectively?
Does this coupling process provide a feasible route, at least
in principle, for the phosphorylation of glucose in the cell?
Explain.
(d) Although coupling ATP hydrolysis to glucosephosphorylation makes thermodynamic sense, how this
coupling
is to take place has not been specified. Given that coupling requires a common
intermediate, one conceivable route is
to use ATP hydrolysis to raise the intracellular concentration of H2PO4- + HPO42- and thus drive the unfavorable
phosphorylation of glucose by H2PO4- + HPO42-. Is this ~i reasonable route? (Think about the
solubility products
of metabolic intermediates.)
(e) The ATP-coupled phosphorylation of glucose is catalyzed in hepatocytes by the enzyme glucokinase.
This
enzyme binds ATP and glucose to form a glucose-ATP-enzyme
complex, and the phosphoryl group is
transferred directly from ATP to glucose. Explain the advantages
of this route.
10. Calculations of  G° for ATP-Coupled
Reactions From data in Table 1-2 calculate the
G° for ATP-Coupled
Reactions From data in Table 1-2 calculate the  G° value
for
G° value
for
the reactions:
(1o)
PhosphCreatine- + H2O<=>Creatine + H2PO4- ; G°1o =
-43.095 kJ/mol
G°1o =
-43.095 kJ/mol
 G°1`=
G°1`= G°1o+G°HPO4+G°H3O+-G°H2PO4-G°H2O= 43.095 + (-1282) + (-284.7) - (-1323) - (-306.7) = 20.011 kJ/mol
G°1o+G°HPO4+G°H3O+-G°H2PO4-G°H2O= 43.095 + (-1282) + (-284.7) - (-1323) - (-306.7) = 20.011 kJ/mol
(1) PhosphCreatine- + 2 H2O<=>Creatine + HPO42- + H3O+ ; G°1 = 20.011
kJ/mol
G°1 = 20.011
kJ/mol
(2) ADP3-+HPO42-+H3O+<=>ATP4-+2H2O
;  G°2 =
-32.606 kJ/mol
G°2 =
-32.606 kJ/mol
(a) Phosphocreatine- + ADP3-<=>creatine + ATP4-
; G°a = -12.595 kJ/mol
G°a = -12.595 kJ/mol
DG°o =-79.005+-32.606= -111.611
; 3.8*4.184 = 15.899;
(1bo) fructose + H2PO4-<=>fructose
6-phosphate- + H2O ; G°1bo =
-15.899 kJ/mol
G°1bo =
-15.899 kJ/mol
 G°1b`=
G°1b`= G°1bo+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -15.899 + (-1282) + (-284.7) - (-1323) - (-306.7) = -79.005 kJ/mol
G°1bo+G°HPO4+G°H3O+-G°H2PO4-G°H2O= -15.899 + (-1282) + (-284.7) - (-1323) - (-306.7) = -79.005 kJ/mol
(1) fructose 6-phosphate- + 2 H2O<=>fructose
+ HPO42- + H3O+ ; G°1b =
-79.005 kJ/mol
G°1b =
-79.005 kJ/mol
(2) ADP3-+HPO42-+H3O+<=>ATP4-+2H2O
;  G°2b =
-32.606 kJ/mol
G°2b =
-32.606 kJ/mol
(b) ATP4-+
fructose<=>ADP3- + fructose 6-phosphate-
; G°b = -111.6 kJ/mol
G°b = -111.6 kJ/mol
11. Coupling ATP Cleavage to an Unfavorable
Reaction.
To explore the consequences of coupling ATP
hydrolysis under physiological conditions to a thermodynamically
unfavorable biochemical reaction, consider the hypothetical transformation X => Y, for
which  G° 20 kJ/mol.
G° 20 kJ/mol.
(a) What is the ratio [Y]/[XI
at equilibrium? K°o = 3.135•10-4
(b) Suppose X and Y participate in a
sequence of reactions during which ATP4- is hydrolyzed to ADP3-
and H2PO4-,
The overall reaction is :
(1) X<=>Y
;  G°o1 =
20 kJ/mol
G°o1 =
20 kJ/mol
(2) ATP4- + H2O<=>ADP3- + H2PO4- ; K°o = 220409 ;  G°o2 = -30.500 kJ/mol
G°o2 = -30.500 kJ/mol
X + ATP4- + H2O<=>Y + ADP3- + H2PO4- ;  G°o =
G°o =  G°o1+G°o2 = DG°o = 20+(-30.5) = -10.500 kJ/mol
G°o1+G°o2 = DG°o = 20+(-30.5) = -10.500 kJ/mol
K°eqo=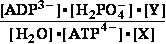 =69.1 ; K°eqo•[H2O] =
=69.1 ; K°eqo•[H2O] = = 3810
= 3810
 =
=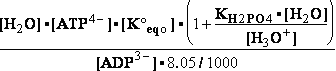 =1.994•106;[H2PO4-]=
=1.994•106;[H2PO4-]=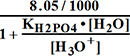
Pi=8.05 mM=[H2PO4-]+[HPO42-]
; [H2PO4-]=8.05/1000-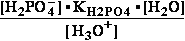 ;
;
Calculate [Y]/[X] for this reaction at
equilibrium. Assume that the concentrations of [ATP4-], [ADP3-], and
([H2PO4-]+ [HPO42-])are all 1 M when the reaction is at equilibrium T = 310.16 °K.
(c) We know that [ATP4-], [ADP3-], and [H2PO4-l are not 1 M under physiological conditions. Calculate
[Y]/[X] for the ATP-coupled reaction when the values of
[ATP4-], [ADP3-], and [H2PO4-l are those found
in rat myocytes (Table 1-3).
12. Calculations of  G at Physiological
Concentrations.
G at Physiological
Concentrations.
Phosphocreatine- + ADP3-<=>creatine + ATP4-
; G° = -12.5 kJ/mol -43+30.5
G° = -12.5 kJ/mol -43+30.5
 G=
G= G°+R•T•ln
G°+R•T•ln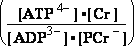 = -12500+RF*T*ln(2.6*1/0.73/4.7)= 13215.2 -13.215 kJ/mol at T =
310.16 K
= -12500+RF*T*ln(2.6*1/0.73/4.7)= 13215.2 -13.215 kJ/mol at T =
310.16 K
at 37°C as it occurs in the cytosol of neurons, in which phosphocreatine- is present at [PCr-]=4.7mM,
creatine at [Cr]=1.0 mM, ADP3-
at 0.73 mM, and ATP4- at 2.6 mM.
13. Free
Energy Required for ATP Synthesis under Physiological Conditions.
In the cytosol of rat hepatocytes,
the mass-actionratio is :
R°o=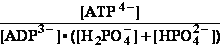 = 5.33•10-2 M-1 ; at 37°C T = 310.16 K
= 5.33•10-2 M-1 ; at 37°C T = 310.16 K
Pi = [H2PO4-]+[HPO42-] ; [H2PO4-] =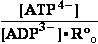 -
-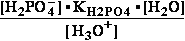 ;
;
[H2PO4-]=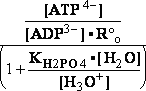 ;
; G=
G= G°+R•T•ln
G°+R•T•ln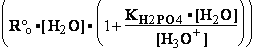 =36.99 kJ/mol
=36.99 kJ/mol
ATP4- + H2O<=>ADP3- + H2PO4- ; K°= 220409 ; G°
= -30.500 kJ/mol
G°
= -30.500 kJ/mol
+30500+RF*T*ln(0.0533*aHOH*(1+2.543489E-9*aHOH/10^(-7.36)))=
36988.76
Calculate the free energy  G required to synthesize ATP4- in a rat hepatocyte.
G required to synthesize ATP4- in a rat hepatocyte.
14. Daily ATP Utilization by Human
Adults.
(a) A total of 30.5 kJ/mol of free energy  G is needed to
synthesize ATP4- from ADP3- and H2PO4- when the
G is needed to
synthesize ATP4- from ADP3- and H2PO4- when the
reactants and products are at 1 M concentration (standard
state). Because the actual physiological concentrations
of ATP4-, ADP3-, and H2PO4-are
not 1 M, the free energy  G required to synthesize ATP4- under physiological
G required to synthesize ATP4- under physiological
conditions is different from  G°.
Calculate the free energy
G°.
Calculate the free energy  G required to synthesize ATP4- m
the human
G required to synthesize ATP4- m
the human
hepatocyte when the physiological concentrations of
ATP4-, ADP3-, (H2PO4-+
HPO42-) are 3.5,1.50, 5.0
mM and pH=7.36, respectively, at 37°C.
K°H2PO4=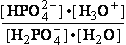 ;Pi = 5 mM=[H2PO4-]+[HPO42-];[H2PO4-]=5 -
;Pi = 5 mM=[H2PO4-]+[HPO42-];[H2PO4-]=5 -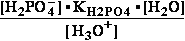
K°H2PO425= 1.1469•10-9;  G° = -R•T•ln(K°H2PO4) = 51.034 kJ/mol at T = 298.16 K
G° = -R•T•ln(K°H2PO4) = 51.034 kJ/mol at T = 298.16 K
K°H2PO437 = EXP(-51033.6/T/RF) = 2.543489•10-9 at T = 310.16 K
[H2PO4-]=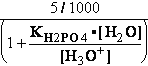 ;
;  G°= -R•T•ln
G°= -R•T•ln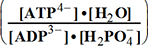 at T = 310.16 K
at T = 310.16 K
 G=
G= G°+R•T•ln
G°+R•T•ln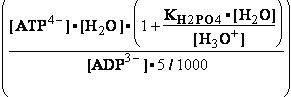 =60.3976 kJ/mol atT
= 310.16 K
=60.3976 kJ/mol atT
= 310.16 K
ATP4- + H2O<=>ADP3- + H2PO4- ; K°= 220409 ;  G°= -30.500 kJ/mol
G°= -30.500 kJ/mol
(b) A 68 kg (150 lb) adult
requires a caloric intake of 2 000 kcal (8 360 kJ) of food per
day (24 h). The food
is metabolized and the free energy  G is used to synthesize ATP4-, which then provides energy
G is used to synthesize ATP4-, which then provides energy  G for the body's
G for the body's
daily chemical and mechanical work W=- G. Assuming that the
efficiency of converting food energy E into ATP4-
G. Assuming that the
efficiency of converting food energy E into ATP4-
is 50%, calculate the weight mATP of ATP4- used by a human adult in 24 h. What percentage of the body weight
does this represent?
nATP = 8360/60.397598/2 = 69.208
mol ; mATP = nATP•MATP = 69.208050*506.91 = 35082 g
(c) Although adults synthesize large
amounts of ATP4- daily, their
body weight, structure, and composition do not
change significantly during this period. Explain this apparent contradiction.
15. Rates of Turnover of  and
and  Phosphates of ATP4- A-O-OPO--O-OPO--O-OPO--O-
(A-
Phosphates of ATP4- A-O-OPO--O-OPO--O-OPO--O-
(A-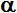 -
-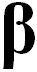 -
-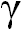 -O-).
-O-).
If a small amount of ATP4- labeled with radioactive phosphorus in
the terminal position, [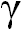 -32P] ATP4-, is added to
-32P] ATP4-, is added to
a yeast extract, about half 1/2 of the 32P activity is found in H2PO4- within a few minutes, but the concentration
of [ATP4-]= const remains
unchanged. Explain. If the same experiment is carried out using ATP4- labeled with 32P
in the central position, [ -32P] ATP4-, the 32P does not appear in H2PO4- within such a short time.
Why?
-32P] ATP4-, the 32P does not appear in H2PO4- within such a short time.
Why?
16. Cleavage of ATP to AMP and PPi during Metabolism
The synthesis of the activated form of acetate (acetyl-CoA)
is carried out in an ATP-dependent process:
Acetate + CoA4-<=>acetyl-CoA4- + H2O
;  G°1 = 31.4 kJ/mol
G°1 = 31.4 kJ/mol
ATP4- + H2O<=>AMP2-
+ PPi2- ;  G°2 = -45.6 kJ/mol
G°2 = -45.6 kJ/mol
Acetate + CoA + ATP4-<=>acetyl-CoA + AMP2- + PPi2- ;  G° = -45.6+31.4 = -14.2= -14.2 kJ/mol
G° = -45.6+31.4 = -14.2= -14.2 kJ/mol
(a) The  G° for the hydrolysis of acetyl-CoA to acetate and CoA is -31.4 kJ/mol and that for hydrolysis
G° for the hydrolysis of acetyl-CoA to acetate and CoA is -31.4 kJ/mol and that for hydrolysis
of ATP4- to AMP2- and PPi2-
is -45.6 kJ/mol. Calculate  G° for the ATP-dependent synthesis of acetyl-CoA.
G° for the ATP-dependent synthesis of acetyl-CoA.
(b) Almost all cells contain the enzyme inorganic pyro-phosphates,
which catalyzes the hydrolysis of PPi2- to H2PO4-.
What effect does the presence of this enzyme have on the synthesis of acetyl-CoA?
Explain!
H2PO3-O-O3PH22-
+ H2O<=>2 H2PO4-;  G°PP = -19 kJ/mol ;
G°PP = -19 kJ/mol ; G°total =
G°total =  G° +
G° +  G°PP = -45.6+31.4 = -14.2-19= -33.2
kJ/mol
G°PP = -45.6+31.4 = -14.2-19= -33.2
kJ/mol
H2PO3-O-O3PH22- + 3 H2O<=>2 HPO42- + 2 H3O+ ;  G°PPH = 107.21 kJ/mol
G°PPH = 107.21 kJ/mol
17. Energy for H3O+ Pumping The parietal cells of the stomach lining
contain membrane ''pumps'' that transport
hydrogen ions H3O+ from the cytosol of these
cells (pHplasma 7.36) into
the stomach, contributing to the acidity
of gastric juice (pHstomach 1.2). Calculate the free energy required to transport 1 mol of
hydrogen H3O+ ions through
these pumps. (Hint: See Oxidative Phosphorylation.)
Assume a temperature of 37°C or T = 310.16 °K. 1445440
H3O+plasma<=>H3O+stomach ; Keq = [H3O+stomach]/[H3O+plasma]=10-pHplasma/10-pHstomach=1.445•106
 G° =
-R•T•ln(Keq) =-36577 = -36.577 kJ/mol
G° =
-R•T•ln(Keq) =-36577 = -36.577 kJ/mol
18. Standard Reduction Potentials The standard reduction potential, E°, of any RedOx pair is defined for the
half-cell reaction in equilibrium of each RedOx system:
Oxidizing agentn+ + n electrons-<=>reducing agent
The E° values for the NAD+/NADH and pyruvate/lactate conjugate RedOx pairs are -0.113 and 0.2291 V,
respectively
but at 37° C degree (310.15 K) E°37: -0.059 and 0.3193
V.
(a) Which conjugate pair has the greater tendency to
lose electrons? Explain.
(b) Which is the stronger oxidizing agent? Explain.
(c) Beginning with 1 M concentrations of each reactant and product at pH 7.36, in which direction will the
following reaction proceed?
Pyruvate-+H3O+ +NADH=>lactate-+NAD++ H2O; (E°NADH-E°pyruvate)•F•2= G°= -73.000
kJ/mol
G°= -73.000
kJ/mol
 G=
G=  G° +
R•T•ln
G° +
R•T•ln = -18.957
kJ/mol favorable direction of reaction
= -18.957
kJ/mol favorable direction of reaction
(d) What is the standard free-energy
change ( G°) at 37 °C for the conversion of pyruvate to lactate
G°) at 37 °C for the conversion of pyruvate to lactate
(e) What is the equilibrium constant (Keq) for this reaction?
Keq= =6.149•1012 ; pH•Keq=
=6.149•1012 ; pH•Keq=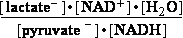 =268417
=268417
19. Energy Span of the Respiratory Chain Electron e- transfer in the mitochondrial respiratory chain
may be represented by the net reaction equation
2 NADH + 2 H3O+ + O2=> 2 NAD+ + 4 H2O (E°NADH- E°O2)•F•4 =  G° = -552.74 kJ/mol
G° = -552.74 kJ/mol
(a) Calculate the value of  E° for the net
reaction of mitochondrial electron e- transfer at 37°C.
E° for the net
reaction of mitochondrial electron e- transfer at 37°C.
(b) Calculate  G° for this reaction.
G° for this reaction.
 E° = E°NADH-
E°O2 = -0.059-1.3732 = -1.4322 V
E° = E°NADH-
E°O2 = -0.059-1.3732 = -1.4322 V
(c) How many nATP molecules can
theoretically be generated by this reaction if the free energy of ATP synthesis
under cellular conditions is 52 kJ/mol? n =
10.63
20. Dependence of Electromotive Force
on Concentrations
Calculate the electromotive force EMF (in volts V)
registered by an electrode immersed in a solution containing
the following mixtures of NAD+and NADH at pH 7.36 and 37 °C, with reference to a half-cell
of E° 0.00 V.
NADH + H2O<=>NAD+ + H3O+ + 2e- E37 = -0.0590 V (David Harris)
EMF = E = E37 + R•T/F/2•ln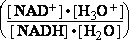 = -0.36983 V
= -0.36983 V
(a) 1.00 mM NAD+ and 10.0 mM NADH; E = -0.36983
V
(b) 1.00 mM NAD+ and 1.00 mM NADH ; E = -0.33906 V
(c) 10.0 mM NAD+ and 1.00 mM NADH ; E = -0.30829 V
21. Electron Affinity of Compounds List
the following substances in order of increasing tendency to accept
electrons e- at pH=7.36 by RedOx potential Eo values:
O2g+4 H3O++ 4 e-= 6 H2O Suchotina;
Eo = 0.8130 V ; E37 = 1.3732 V
O2aq+2H3O++2e-=H2O2aqua+
2H2O University
Alberta; Eo = 0.2336 V ; E37 = 0.7937 V
oxalo-acetate2-+2H3O+ +2e-= Malate2-+2H2O CRC ; Eo = -0.2225 V ; E37 = 0.3376 V
O2g+ e- =
O-2aq Suchotina;
Eo = -0.2355 V ; E37 = -0.2355 V
NADP++H3O+ +2e-= NADPH + H2O CRC ;
Eo = -0.3429 V ; E37 = -0.0629 V
a-Ketoglutarate+CO2+2H3O++2e-=
isocitrate+2H2O
; Eo = -0.4283 V ; E37 = 0.13185 V
(a) a-keto-glutarate + CO2 (yielding iso-citrate); (b)
oxalo-acetate; (c) O2 ; (d) NADP+.
22. Direction of Oxidation-Reduction
Reactions
Which of the following reactions would you expect to proceed
in the direction shown under standard conditions
pH=7.36 and 37°C, assuming that the appropriate enzymes are
present to catalyze them?
(E°Red-E°Ox)•F•n =  G° kJ/mol
;
G° kJ/mol
;
 G=
G=  G°+
R•T•ln
G°+
R•T•ln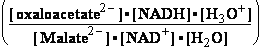 = 10.053
kJ/mol unfavorable direction => for (a)
= 10.053
kJ/mol unfavorable direction => for (a)
(a) Malate2-+ NAD++
H2O => oxalo-acetate2-+NADH+H3O+;(E°malate-E°NAD+)•F•2
=  G°= 53.756
kJ/mol
G°= 53.756
kJ/mol
 G=
G=  G° -
R•T•ln(10-7.36)
= 0.568 kJ/mol <= direction
G° -
R•T•ln(10-7.36)
= 0.568 kJ/mol <= direction
favorable to left for (b)
(b) aceto-acetate- + NADH + H3O+ => b-hydroxy-butyrate- + NAD+ + H2O ;  G°= -43.135 kJ/mol
G°= -43.135 kJ/mol
 G=
G=  G° -
R•T•ln(10-7.36)
= -29.298 kJ/mol => direction
G° -
R•T•ln(10-7.36)
= -29.298 kJ/mol => direction
favorable to right
(c) Pyruvate- + NADH + H3O+ => lactate- + NAD+ + H2O ;  G°= -73.001 kJ/mol => direction
G°= -73.001 kJ/mol => direction
(d) Pyruvate- + b-hydroxy-butyrate- => lactate- +
aceto-acetate- ;  G°=
-29.866 kJ/mol => direction
G°=
-29.866 kJ/mol => direction
(e) Malate- + pyruvate- => oxalo-acetate- + lactate-
;  G°= 3.526 kJ/mol <= direction
G°= 3.526 kJ/mol <= direction
(f ) Acetaldehyde + succinate2-=> ethanol + fumarate2-
;  G°= 46.447
kJ/mol <= direction
G°= 46.447
kJ/mol <= direction
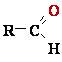 +
4
+
4  + Cu
+ Cu







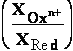
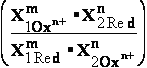 , where
equilibrium (10)
, where
equilibrium (10)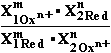 is the ratio as a multiple products over initial compounds concentrations.
is the ratio as a multiple products over initial compounds concentrations. 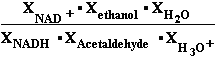 =K
=K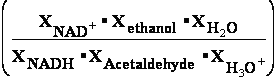
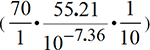 = -6680 J/mol
= -6680 J/mol  + 2e-
+ 2e- or=>
or=> 

 +e-+H
+e-+H +e-+H
+e-+H
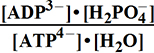 =K°
=K°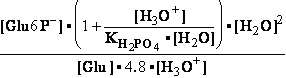 =2.0119•10
=2.0119•10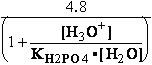 ; [Glu6P-]
=
; [Glu6P-]
=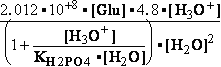 = 1.0574•10-5M
= 1.0574•10-5M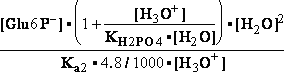 = 23.64M at pH=7.36
= 23.64M at pH=7.36 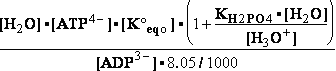 =1.994•
=1.994•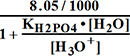
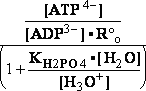 ;
;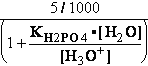 ;
; 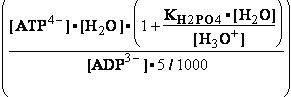 =60.3976 kJ/
=60.3976 kJ/