 Figure 1.
Figure 1. A metabolism for copper ions is widespread among living systems. To help in the
understanding of the binding of the ion in biopolymers and physiological fluids, the
prototype compounds of cupric ions with amino acids have been extensively studied.
Bis (glycinato)copper(II).hydrate was first isolated in 1841 and in 1890 a second form was
discovered. It was later suggested that the two modifications; one pale blue needles and
the other bluish violet glistening plates were geometric (cis/trans) isomers.
These compounds represent some of the first geometric isomers discovered and recently the
novel solid state thermal isomerisation of the cis- to the trans- form was reported.
In this experiment, the formation of the copper(II) glycine complexes will be studied as a
function of pH and from the titration data the overall stability constant b2 will be
calculated. In addition, IR spectroscopy will be used in conjunction with a simple group
theory approach to distinguish between the cis- and trans- isomers of Cu(gly)2·H2O.
The formation of metal complexes is often highly dependent on the pH of the solution. This is because there is a competition for the ligand between the metal ion and the proton as they both bind to the same atoms of the ligand. For glycine at low pH, the metal ion has to displace a proton from the amine N in order to form a stable complex.
Cu2+(aq) + 2NH3+-CH2COO- <-> Cu(H2N-CH2-COO)2 + 2H+(aq)
The number of protons displaced through chelate formation can be determined from a pH titration of a mixture of ligand and metal ion; in this instance a 2:1 mixture of glycine and Cu2+(aq) is used. It is also necessary to do a pH titration of glycine alone, so that the dissociation constants of the ligand can be obtained.
For the ligand:
NH3+-CH2COOH <-> NH3+-CH2COO-(gly-) + H+(aq) Ka1
NH3+-CH2COO- <-> NH2-CH2COO- + H+(aq) Ka2
The stepwise stability constants K1 and K2 for the reaction of the ligand with Cu2+ are given by the expressions:
Cu2+ + gly- <-> Cu(gly)+ K1 (beta1) Cu(gly)+ + gly- <-> Cu(gly)2 K2
and the overall stability constant Beta2 = K1 · K2
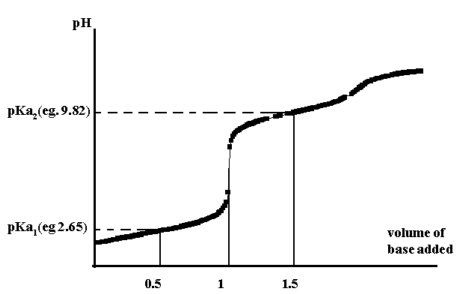
From the titration curve for glycine, the pH at 0.5 the equivalence point gives pKa1 while at 1.5 gives pKa2.
To calculate the stability constants (K1 and K2) use is made of the formation function, n, which is defined as the ratio of total ligand bound to the total metal present:
n = [Cu(gly)+] + 2[Cu(gly)2] / ( [Cu2+] + [Cu(gly)+] + [Cu(gly)2] )
substituting from equations (1) and (2) gives
n = ß1(gly ) + 2ß2 [gly ]2 / (1 + ß1(gly ) + ß2 [gly ]2)
From an experimental standpoint, this needs to be expressed in terms of total copper(II) ions, total glycine and pH for the calculation to be able to be carried out. When this is done, the expression becomes:
[Hgly] = [Hgly]total [H+] [Na+]+ [OH ] / (1+[H+]/Ka1)
and n = [Hgly]total [Hgly]·{1+Ka2/[H+]+[H+]/Ka1} /[Cu2+]total
also [gly-] = Ka2·[Hgly]/[H+]
if n versus p(gly-) is plotted, then an approximate value of the stepwise formation constants, K1 and K2, are obtained at =0.5 and =1.5. A more accurate measure of Beta2 is obtained at =1.0.
A more precise method uses a simple linear least squares analysis of the titration results and makes use of the equation:
n = ß1[gly ] + 2 ß2 [gly ]2 / ( 1+ ß1[gly ] + ß2[gly ]2 )
Rearrangement of which gives:
n/( (1-n)[gly-]) = ß1 + ß2 * (2-n ) * [gly-]/ (1-n) Thus a plot of n/((1-n)[gly-]) versus (2-n) [gly-]/(1-n)
should yield a straight line. Most programmable calculators can do a least squares fit,
or it may be possible to use a spreadsheet application such as Excel on a microcomputer.
To download a zipfile containing an Excel worksheet with a template setup, use the link here.
Prepare the following stock solutions:
a) 500 cm3 of 0.1M NaOH. This should be standardised with potassium hydrogen phthalate. b) 500 cm3 of 0.1M HNO3. This should be standardised with the 0.1M NaOH above. c) 10 cm3 of 0.1M Cu(NO3)2 solution from 0.25g Cu(NO3)2 2.5 H2O. d) 250 cm3 of 0.05M KNO3.
Weigh (to the nearest 0.1mg) a 0.1g sample of glycine into a 250 cm3 beaker. Pipette 100 cm3 of 0.05 KNO3 into the beaker, mix and record the pH. Pipette 10 cm3 of standardised 0.1M HNO3 into the beaker and record the new pH of the solution. Titrate the solution with the standardised 0.1M NaOH, making sure to stir continuously after each addition and to plot the titration curve AS YOU PROCEED. Continue the titration until the number of moles of base added is equal to the number of moles of HNO3 plus the number of moles of glycine present.
Weigh (to the nearest 0.1mg) a 0.1g sample of glycine into a 250 cm3 beaker. Pipette 100 cm3 of 0.05 KNO3 into the beaker, mix and record the pH. Add by pipette, 2 cm3 of 0.1M copper(II) solution and record the pH again. Titrate, using ~ 0.2 cm3 increments of standard 0.1M NaOH, with continuous stirring. Note: the calculations give the best results when the first five or six data points from the titration curve are used.
Copper(II) acetate monohydrate (0.01 mole, 2.0 g) is dissolved in 25 cm3 of hot water. 25 cm3 of hot ethanol is added and the solution kept hot. Glycine(0.02 mole, 1.5 g) is dissolved in 25 cm3 of hot water. The solutions are mixed while hot (~70C) and the solution then cooled on ice. A needle-like precipitate is obtained. Record the yield. Preserve the filtrate.
Two methods have been used for the preparation of the trans- isomer, but the first
gives the cleaner product.
a) 10 cm3 of the filtrate above is placed in a small flask with ~ 1.5 g of the
cis- isomer and 1 g of glycine. The suspension is heated under reflux for one hour. The
hot mixture is then filtered to give the trans-Cu(gly)2·H2O.
Note that if the mixture all dissolves during the reflux, then the cis-product will
reprecipitate not the trans-.
b) An alternative method, is to place a small quantity of the cis-isomer in an oven at
170¦C for an hour. On cooling in air, this leads to the solid state conversion to the
trans-isomer.
It should be possible to distinguish between the two isomers by considering the
immediate environment around the central metal and assuming that their vibrations are
independent of the motions involving the rest of the atoms of the ligands.
IR spectra (KBr pellet 4400-400 cm-1) in JCAMP-DX format
cis-isomer
trans-isomer
That is, by considering only the Cu and the N and O atoms, the cis-isomer will have C2v
symmetry, whilst the trans-isomer D2h symmetry.
The reducible representations for C2v and D2h are:
and using the reduction formula, then for:
C2v -> 2A1 + 2B2 all bands should be IR active, while for
D2h -> 2A1g + B2u + B3u only the B2u and B3u bands
should be IR active, the 2A1g symmetric bands being Raman active.
It is expected therefore that for the metal-ligand stretching vibrations, 4 bands should be observed in the IR spectrum of the cis-is