| Henderson-Hasselbalch equation and pKa
|
The general dissociation of a weak acid, such as a carboxylic acid, is given by the equation:
 where HA is the protonated form (conjugate acid or associated form) and A- is the unprotonated form (conjugate base, or dissociated form).
where HA is the protonated form (conjugate acid or associated form) and A- is the unprotonated form (conjugate base, or dissociated form).
|
The dissociation constant (Ka) of a weak acid is defined as the equilibrium constant for the dissociation reaction (1) of the acid:

|
| page 11 |  | | page 12 |
The hydrogen ion concentration [H+] of a solution of a weak acid can then be calculated as follows. Equation (2) can be rearranged to give:
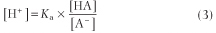 Equation (3) can be expressed in terms of a negative logarithm:
Equation (3) can be expressed in terms of a negative logarithm:
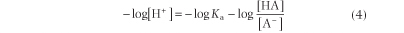 Since pH is the negative logarithm of [H+], i.e. -log[H+] and pKa equals the negative logarithm of the dissociation constant for a weak acid, i.e. -log Ka, the Henderson-Hasselbalch equation (5) can be developed and used for analysis of acid-base equilibrium systems:
Since pH is the negative logarithm of [H+], i.e. -log[H+] and pKa equals the negative logarithm of the dissociation constant for a weak acid, i.e. -log Ka, the Henderson-Hasselbalch equation (5) can be developed and used for analysis of acid-base equilibrium systems:
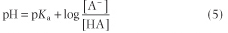 For a weak base, such as an amine, the dissociation reaction can be written as:
For a weak base, such as an amine, the dissociation reaction can be written as:
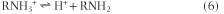 and the Henderson-Hasselbalch equation becomes:
and the Henderson-Hasselbalch equation becomes:
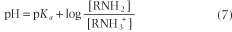 From equations (5) and (7), it is apparent that the extent of protonation of acidic and basic functional groups, and therefore the net charge will vary with the pKa of the functional group and the pH of the solution. For alanine, which has two functional groups with pKa = 2.4 and 9.8, respectively (Fig. 2.4),
the net charge varies with pH, from +1 to -1. At a point intermediate between pKa1 and pKa2, alanine has a net zero charge. This pH is called its isoelectric point, pI (Fig. 2.4).
From equations (5) and (7), it is apparent that the extent of protonation of acidic and basic functional groups, and therefore the net charge will vary with the pKa of the functional group and the pH of the solution. For alanine, which has two functional groups with pKa = 2.4 and 9.8, respectively (Fig. 2.4),
the net charge varies with pH, from +1 to -1. At a point intermediate between pKa1 and pKa2, alanine has a net zero charge. This pH is called its isoelectric point, pI (Fig. 2.4).
|
|