| Mathematical models of aging
|
In the early 19th century, Gompertz observed that the age-specific death rate of humans increased exponentially after 35 years of age, and that human survival curves could be modeled by what is now known as the Gompertz equation:
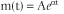where: m is the age specific death rate at age t ;
A is the intercept (death rate at birth); and
αis a slope constant (the effect of time on the death rate).
The Gompertz-Makeham equation: m(t) = Aeαt + B, adds a constant, B, to correct for the age-independent death rate, e.g. as a result of infant mortality or accidents, and provides a better fit to actuarial data.
|
| The Gompertz plots in Fig. 42.2 illustrate the time-dependent changes in death rate for three different species of vertebrates and for flies raised at different temperatures. Shorter-lived mammals have a greater age-adjusted rate of death (α), while the death rate for poikilotherms varies with ambient temperature - flies live longer when grown at lower temperatures. This observation has been interpreted as evidence for 'rate of living' or 'wear and tear' theories of aging. Flies, being more active at higher temperature, consume more energy and die more rapidly. Flies that are restrained, e.g. in a matchbox, rather than a large carboy, also live longer; wingless flies live longer; and male flies, segregated from females, also live longer. In each case, in small enclosures, without wings and in the absence of the opposite sex, male flies are less active, have lower basal metabolic rates, and have longer mean and maximum lifespans.
|
|
